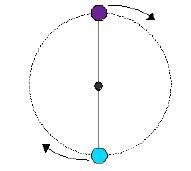
Тело вращается по вертикальному кругу с помощью шнура, прикрепленного в центре круга. С какой минимальной скоростью он должен двигаться в верхней части пути, чтобы шнур был едва натянут, то есть находился на грани обрыва? Предположим, что радиус окружности равен 1 метру.
Ответы
Дано:
R = 1 м
g = 10 м/с²
υ_min - ?
Решение:
Сначала запишем уравнение по Второму закону Ньютона для положения тела в верхней точке его траектории движения. Направим ось Y вниз. На тело действует сила натяжения шнура Т и сила тяжести mg. Ускорение - центростремительное. Равнодействующая сил равна:
Т + mg = ma
a = υ²/R => T + mg = mυ²/R
Выразим квадрат скорости:
υ²*(m/R) = Τ + mg
υ² = R*(Τ + mg)/m = (RT + Rmg)/m = RT/m + Rg = R*(T/m + g)
υ² = R*(T/m + g)
Теперь проанализируем это выражение. Очевидно, чтобы скорость была минимальной, надо чтобы минимальным было значение её выражения. Или, что то же самое, было минимальным значение выражения квадрата скорости, которое мы и рассматриваем. Радиус дан в условиях - он постоянен. Ускорение свободного падения - это тоже константа. Как и масса. А вот сила натяжения шнура должна быть как можно меньшей. Если Т по значению будет как можно ближе к нулю, то ближе к нулю будет и выражение Т/m. Следовательно, мы можем пренебречь этим выражением. Тогда:
υ² = R*(0 + g) = gR => υ = √(gR) = √(10*1) = 3,16... = 3,2 м/с
Ответ: приблизительно 3,2 м/с.