Знайти об’єм тіла, утвореного обертанням навколо осі Ох
фігури обмежені лініями.
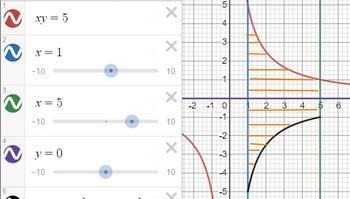
xy=5, x=1,x=5,y=0
Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:
формула для объема тела вращения вокруг оси ОХ
у нас:
рисуем графики и видим, что
b=1; a=5; y= 5/x
и тогда
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
10 лет назад
10 лет назад