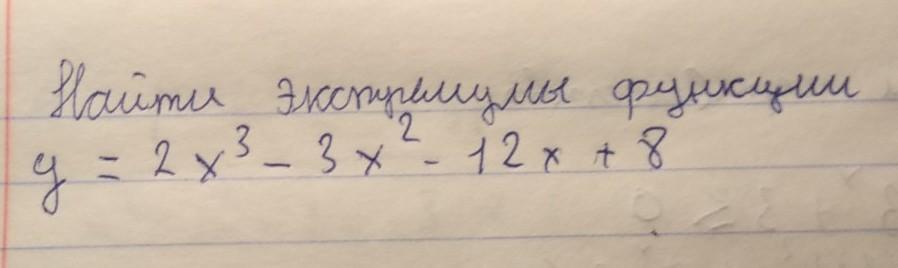Ответы
Ответ дал:
2
Ответ:
x₁=2; y= -12 min
x₂= -1; y= 15 max
Объяснение:
y(2)=16-12-24+8= -12;
y( -1)= -2-3+12+8= 15
Термины: "экстремумы функции" это значение "у" ; "точки экстремума" это значение "Х"
х = -1 максимум. х = 2 минимум.
С учебных порталов. Экстре́мум функции — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума.
Нужно ещё значение У
Теперь оно. Автор вопроса. В ответе значение х не пишите.
Спасибо
Ответ дал:
2
Відповідь:
Пояснення:
Перша прохідна функції:
y' = 6·x^2-6·x-12
6·x^2-6·x-12 = 0
x1 = -1
x2 = 2
__+______-1______-__________2_______+____>y'
зростає max спадає min зростає
Обчислимо значення функції
f(-1) = 15
f(2) = -12
Відповідь:
fmin = -12, fmax = 15
Экстре́мум в математике — максимальное или минимальное значение функции (у) на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума (х)
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад