Помогите, пожалуйста, с высшей математикой. Тема
Интегральное исчисление функции одной переменной
Приложения:
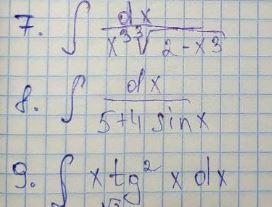
Ответы
Ответ дал:
0
Объяснение:
7.
8.
9.
Вас заинтересует
3 года назад
8 лет назад
10 лет назад