Ответы
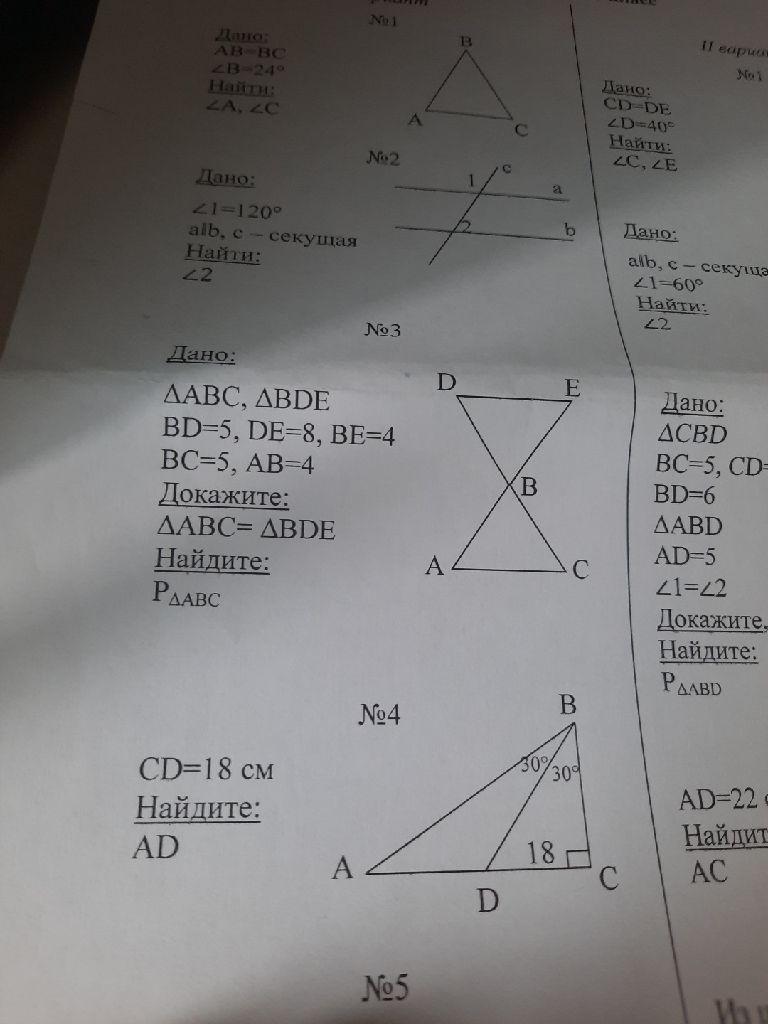
3) Исходя из правила : Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны то у нас две стороны BD=BC=5 ; AB=BE=4 ; и также мы знаем что DBE=ABC равны так как они вертикальные исходя из выше перечисленного они треугольники DBE=ABC равны тогда периметр ABC равен 4)B треугольнике с 30,60,90гр есть свойство наименьший катет А(протеволежит углу 30 ) а другой катет (противолежит углу 60 )√3а гипотенуза равна 2A. В нашем случае нужно найти AC так как AC= AD+DC=> AD=AC-DC тогда так как DC -это наименьший катет (в треугольнике BDC) то есть это a=18 ; а BC -катет противолежащий к углу в 60 гр то тогда BC=√3а=18√3 -этот наименьший катет противолежащий к углу 30 (в треугольнике ABC) то тогда AC= 18√3 *√3 =54 то тогда AD=54-18=36
2) Вертикальный углу 1 тоже равен 120°, и он с углом 2 составляют в сумме 180°, т.к. это внутренние односторонние при а║b и секущей с. Значит, искомый ∠2=180°-120°=60°
3) По первому признаку равенства треугольников ΔАВС=ΔВDE, т.к. у этих треугольников ВD=BC-5, ВЕ=ВА=4, и ∠DBE=∠АВС как вертикальные. Значит, DE=АВ=8, зная три стороны треугольника, найдем его периметр.
Р ΔАВС=4+5+8=17
4) В треугольнике ВСD DC=18, ∠С=90°; ∠ В=30°⇒ ВD=2*18=36
ВС=√(36²-18²)=√((36-18)*(36+18))=18√3; В треугольнике АВС ВС лежит против угла в 30°, т.к. ∠ С=90°, ∠В =30°+30°=60°; значит, АВ=2*ВС=2*18√3=36√3; тогда АС=√(АВ²-ВС²)=√(36²*3-18²*3)=√(18²*3*(2²-1))=
√(18²*3²)=18*3=54, АD=AC-DC=54-18=36