70 баллов за задачу 8 ого класса!!!! В треугольнике ABC угол A равен 66∘. На продолжениях отрезка BC за точки B и C выбраны такие точки X и Yсоответственно, что AB=BX, AC=CY . Найдите уголXIaY, гдеIa — точка пересечения биссектрис внешних углов B и C треугольника ABC.
BMW52:
57°
Подскажите решение
нет , 114 , чего -то никто не хочет решать задачу , а она простенькая
Ну, в задачке есть один довольно забавный "побочный след". Точка Y лежит на окружности описанной вокруг тр-ка ABIa, а точка X - то же для тр-ка ACIa. Ну, или можно так сказать - четырехугольники ABIaY и ACIaX вписанные.
Да ошибка про вписанный.
Ответы
Ответ дал:
4
Ответ:
114° .....................
Объяснение:
Приложения:
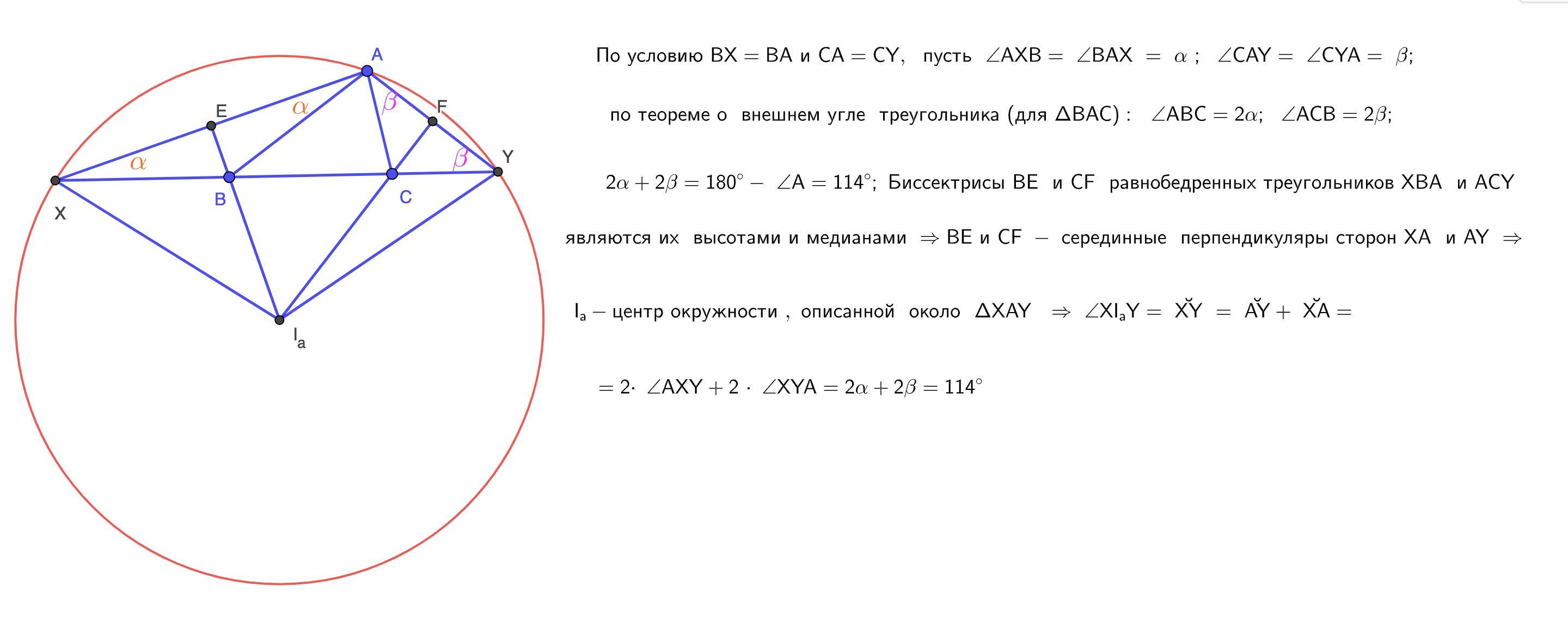
В решении использованы утверждения : центральный угол измеряется дугой , на которую он опирается , а вписанный равен её половине
спасибо
∠BXIa = ∠BAIa = ∠CAIa = ∠CYIa; поэтому YABIa и XACIa вписанные. Это само по себе интереснее, чем вопрос в задаче.
Понятно, что AIa биссектриса ∠BAC :) ну я на всякий случай.
Тут можно еще пофантазировать по мотивам леммы трилистника. Скажем, окружность с центром A касается BC, касательные к ней из точек X и Y пересекутся на IaA.
не пересекутся :) реакция слабая, я думал, будет вал возмущения :)
Слабая?..... 0
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад