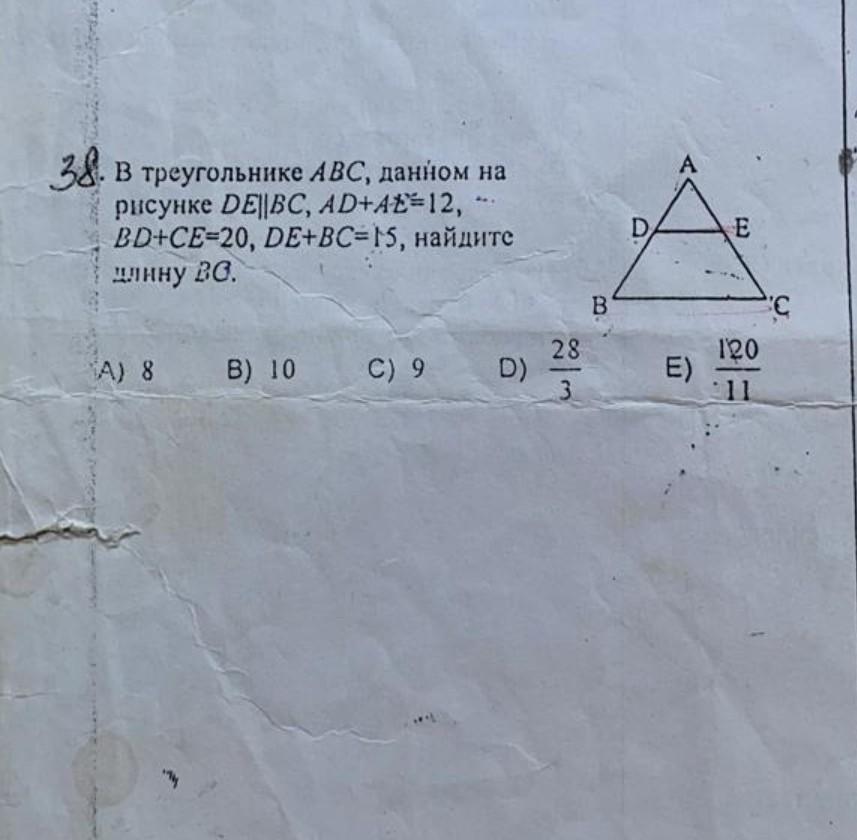
помогите решить пожалуйста
Приложения:
ДжинXо:
С помощью уравнения. ДЕ-средняя линия, и будет в два раза меньше основания треугольника. Получается, ВС=х; ДЕ=х/2. Их сумма равна 15. Уравнение: х+х/2=15; 2х/2+х/2=15; 2х+х/2=15; 3х/2=15; 2*3х/2=2*15; 3х=2*15; 3х=30; х=30/3; х=10.
Ответ В)10
А где в условии сказано, что ДЕ средняя линия?
Там только параллельность. Ну и значит есть подобные треугольники
спасибо большое
А вам только ответ?
Ну вроде средняя линия параллельна основанию. Значит я решила методом исключения
решение тоже нужно
Извините
Это не средняя линия. Иначе бы суммы AD + AE = BD + CE. Получается 12 = 20. Значит DE - не средняя линия.
Ответы
Ответ дал:
3
Відповідь:
Е) 120/11
Покрокове пояснення:
Треугольники ADE и ABC подобны. Так как угол при вершине A одинаков для обоих треугольников, а углы при основании D = B, а E = C, так как DE || BC.
У подобных треугольников с коэффициентом подобия к все стороны относятся друг к другу с таким коэффициентом.
AB = AD × k
AC = AE × k
BC = DE × k
Значит
( AD + AE ) × k = AB + AC
AD + AE = 12
BD + CE = 20
Значит
AB + AC = 20 + 12 = 32
Сумма боковых сторон треугольников ADE и ABC относятся друг к другу как 12 к 32, следовательно и основания этих треугольников DE и BC будут друг к другу как 12 к 32.
DE + BC = 15
Сумма отношений сторон DE и BC друг к другу:
12 + 32 = 44
Создадим пропорцию:
15 / 44 = BC / 32
BC = 15 × 32 / 44 = 480 / 44 = 120/11
Про подобие не написали.
и нет доказательства того, что если сумма боковых сторон подобных треугольников относятся друг к другу как a:b, то и основания этих треугольников будут относиться друг к другу как a:b .
Это следует из подобия.
это надо доказывать, т.к. в учебниках такой теоремы нет
Исправил все, что вы указали. Спасибо за замечания.
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад