Question

помогите с решением,,,,,,,,

Answer 1

Ответ:  4(кв.ед).

Пошаговое объяснение:

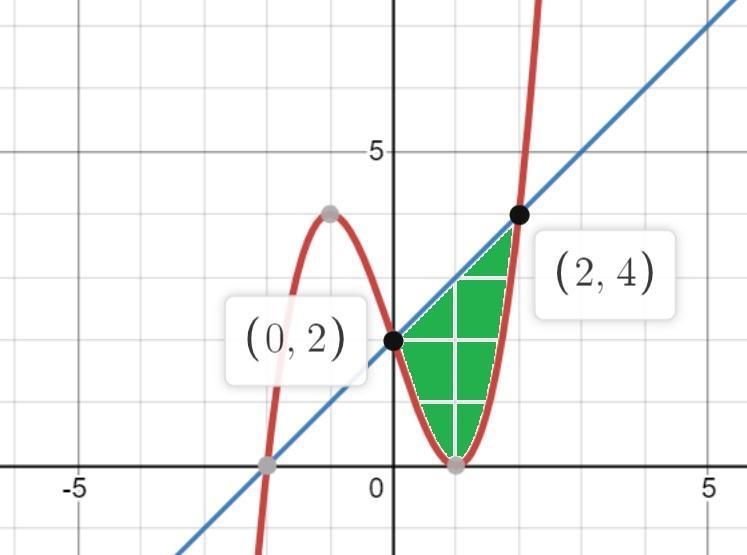
Пределы интегрирования от 0 до 2  находим решением системы уравнений y=x³-3x+2 и y=x+2;

x+2=x³-3x+2;

x³-4x=0;

x(x²-4)=0;

x1=0;

x²-4=0;

x²=4;

x=±2;

---------------

Так как заштрихованная часть графика функции находится в положительной зоне, то пределы интегрирования равны  от 0 до 2.

------------------

Площадь S=∫₀²(x+2-x³+3x-2)dx=∫₀²(4x-x³)dx=4∫₀²xdx-∫₀²x³dx=

=4/2x²|₀²-1/4x⁴|₀²=2*4-1/4*16=8-4=4(кв.ед).

(См скриншот)