Найти такие значения а , для которых корни уравнения
Log(2) ( x+3) -2 Log(4) x= a
были бы расположены между числами 3 и 4
antonovm:
x >0 ; log (2) ( ( x+3)/x) = a ; (x+3)/x = b ( b = 2 ^a ) ; x = 3 /(b-1) ; b > 1 ; 3 < 3 /(b-1) < 4 ....
Ответы
Ответ дал:
2
ОДЗ:
Здесь можно уже не использовать сложные преобразования, а внимательно всмотреться в выражение по-центру. Оно будет больше единицы при , то есть
. В силу монотонности показательной функции:
Нашли верхнюю границу .
Рассмотрим неравенство . Поскольку
в силу
, мы можем перемножить крест-накрест, изменив при этом знак:
Нашли нижнюю границу .
Ответ:
Проверка решения на скриншотах (если вы понимаете, почему там именно так записано, то есть умеете проверять решения с помощью программ для построения графиков).
Приложения:
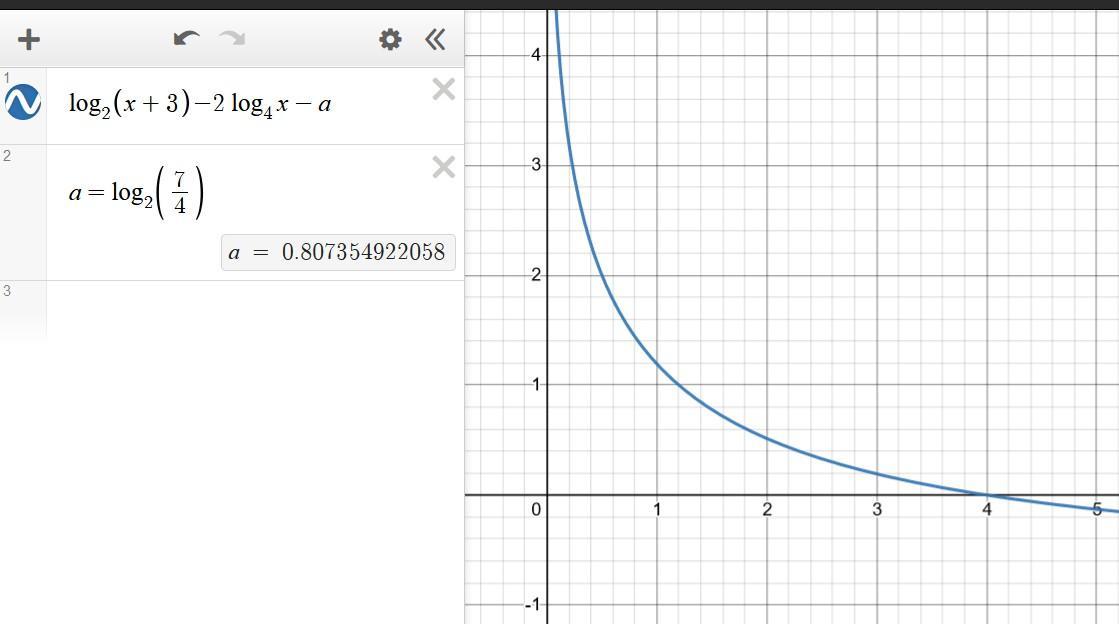
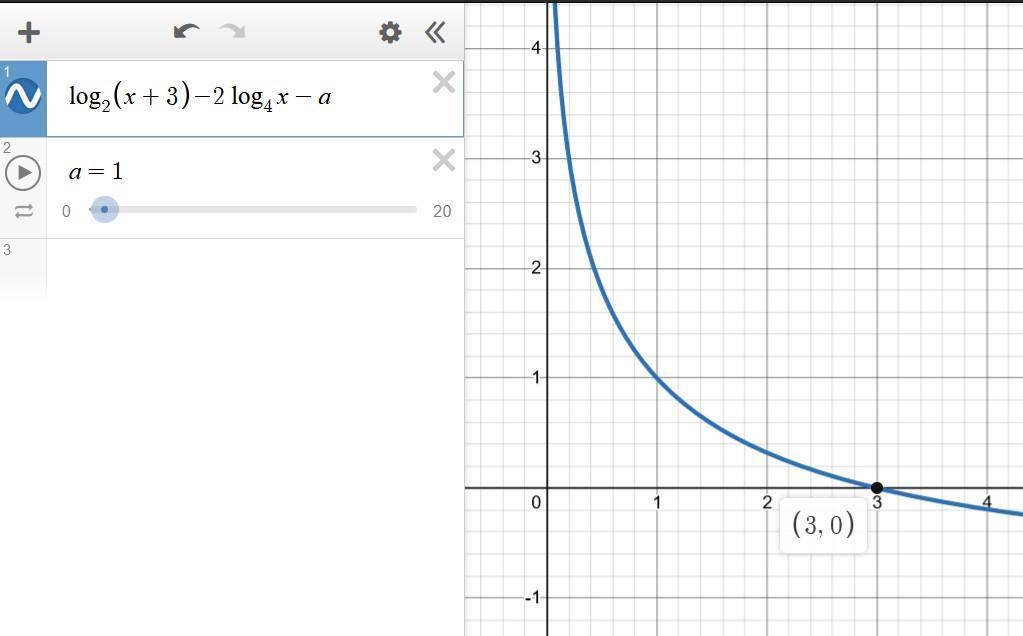
Одз Х>0
Почему 3 <Х<4 ?
Потому что в условии сказано, что корни должны делать между 3 и 4. Ваш кэп.
x>0 потому, что икс стоит под логарифмом
лежать*
А, я не дописал x>0, вы правы
Блин, ведь точно.!!!!!! Спасибо гений20!
Пожалуйста)
А с ОДЗ вы правы: x>0
Решите( помогите) , если знаете, вопросы в профиле.....
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад