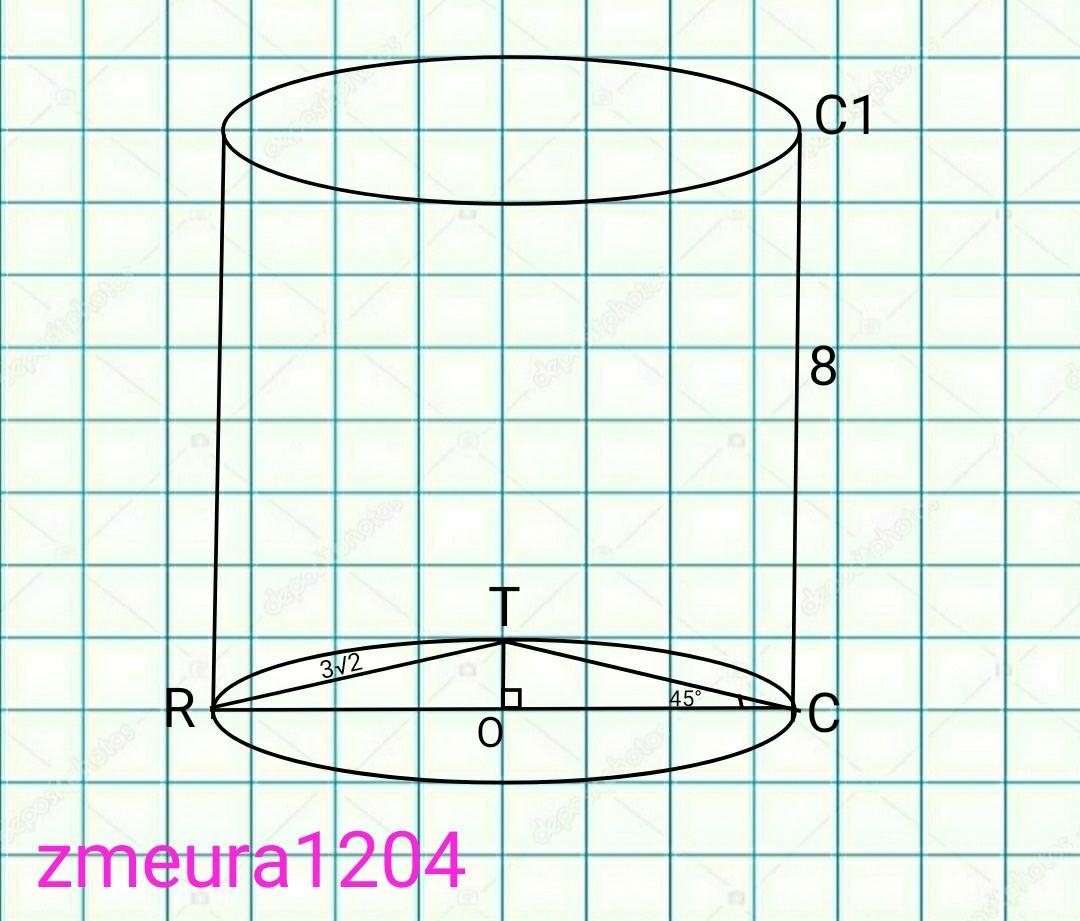
На окружности нижнего основания прямого цилиндра
Выбраны точки R, C, Т. На окружности верхнего основания
цилиндра взята точка C1, причем СС1 – образующая цилиндра,
RC - Диаметр основания. Известно, что
угол RCT = 45 градусов
RT = 3 корня из 2
CC1=8
найдите расстояние от точки T до прямой Rc
график и решение
пожалуйста выручайте
Ответы
Ответ дал:
1
Ответ:
Расстояние от точки Т до прямой RC равно 3.
Объяснение:
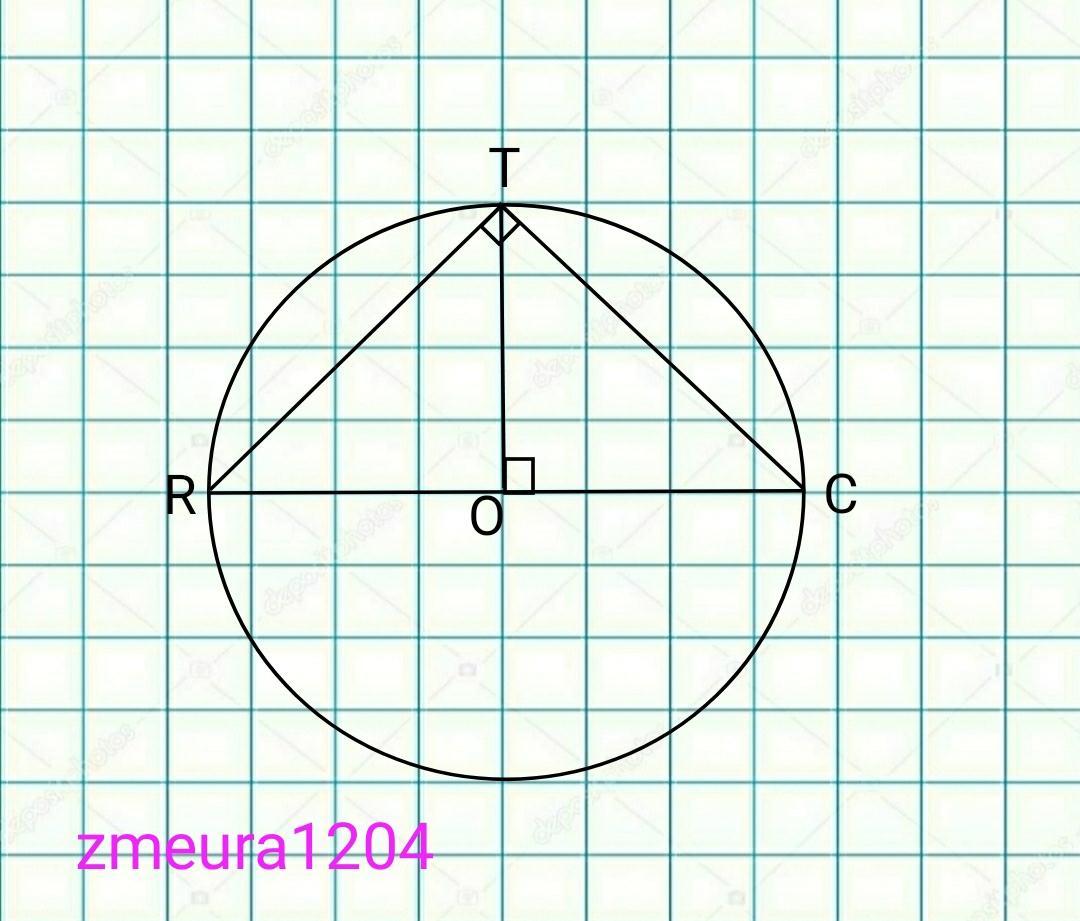
∆RTC- прямоугольный равнобедренный треугольник.
<RTC=90°, так как опирается на диаметр RC.
<RCT=45°, по условию.
В прямоугольном треугольнике сумма острых углов равна 90°
<ТRC=90°-<RCT=90°-45°=45°
Углы при основании равны треугольник равнобедренный.
RT=TC=3√2.
По теореме Пифагора найдем гипотенузу
RC=√(RT²+TC²)=√((3√2)²+(3√2)²)=√(18+18)=
=√36=6
Так как ∆RTC- равнобедренный, то ТО- высота, медиана и биссектрисса.
Медиана равна половине гипотенузы.
ТО=1/2*RC=1/2*6=3.
Приложения:
kiusupov16:
спасибо
Пожалуйста.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
10 лет назад