Question

Алгебра, 11 клас, рівняння з параметром

Answer 1

Ответ:

(см. объяснение)

Объяснение:

$\sqrt{a+\sqrt{a+x}}=x$

Если я правильно понял, то нужно решить уравнение при каждом значении параметра.

Возведем обе части уравнения в квадрат на условии, что $x\ge0$.

$a+\sqrt{a+x}=x^2\\\sqrt{a+x}=x^2-a$

Возведем обе части уравнения в квадрат, добавив условие $a\le x^2$.

$a+x=x^4-2ax^2+a^2\\a^2-a(2x^2+1)+x^4-x=0$

Решаем через дискриминант:

$D=(2x^2+1)^2-4(x^4-x)=4x^2+4x+1=(2x+1)^2\\\sqrt{D}=2x+1$

Найдем корни:

$\left[\begin{array}{c}a=x^2+x+1\\a=x^2-x\end{array}\right;$

Итого исходному уравнению равносильно:

$\left\{\begin{array}{c}x\ge0\\a\le x^2\\\left[\begin{array}{c}a=x^2+x+1\\a=x^2-x\end{array}\right\end{array}\right;$

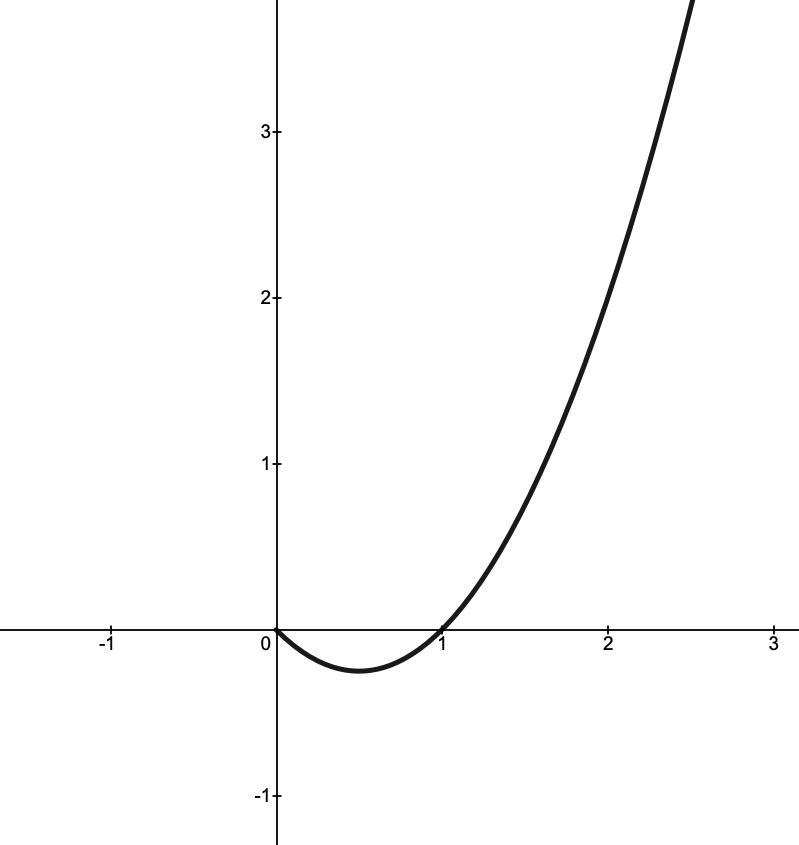
Строим все в координатах (x; a):

(см. прикрепленный файл)

Итого:

• При $a\in\left\{-\dfrac{1}{4}\right\}\cup(0;\;+\infty)$ исходное уравнение имеет единственное решение.
• При $a\in\left(-\dfrac{1}{4};\;0\right]$ исходное уравнение имеет ровно два различных решения.
• При $a\in\left(-\infty;\;-\dfrac{1}{4}\right)$ исходное уравнение не имеет решений.

Задание выполнено!