Question

ПРОШУ ПОМОГИТЕ!!!ЭТО РЕАЛЬНО ОЧЕНЬ СРОЧНО!!!!ДАЮ ВСЕ СВОИ БАЛЛЫ!!!

Answer 1

Через точку А провели пять прямых . Затем провели шестую прямую , не проходящую через точку А. Какое наибольшее количество треугольников Могло получиться? Как провести шестую прямую , чтобы количество образовавшихся треугольников было наименьшим.

Решение

Пусть О-точка пересечения пяти прямых.

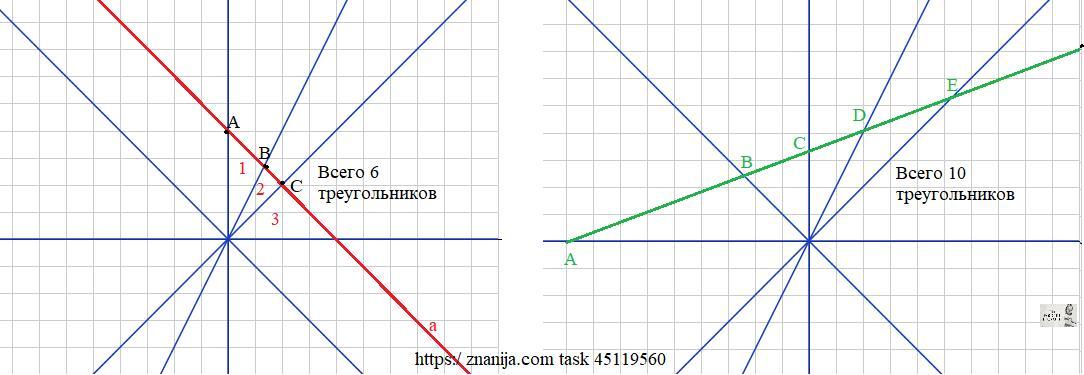
Если провести  шестую прямую , не проходящую через точку А и пересекающую все пять прямых , то наибольшее количество треугольников будет 10:

- с вершиной А  4 штуки:

- с вершиной В 3 штуки:

- с вершиной С 2 штуки:

- с вершиной D 1 штуки.

Чтобы количество образовавшихся треугольников было наименьшим , шестую прямую надо провести параллельно любой прямой из пяти. Количество треугольников будет 6.