Question

50 БАЛЛОВ. ПОМОГИТЕ СРОЧНО при каком наименьшем значении параметра a в уравнение x^3-8/x-2=a имеет ровно один корень​

Answer 1

Ответ:   a=3 .

$\dfrac{x^3-8}{x-2}=a\ \ ,\ \ \ \ ODZ:\ x\ne 2\ ,\\\\\dfrac{(x-2)(x^2+2x+4)}{x-2}=a\ \ \Rightarrow \ \ \ \ x^2+2x+4=a\ ,\ x\ne 2\ \ ,\\\\x^2+2x+(4-a)=0\\\\D=b^2-4ac=2^2-4(4-a)=4-16+4a=4a-12=4(a-3)$

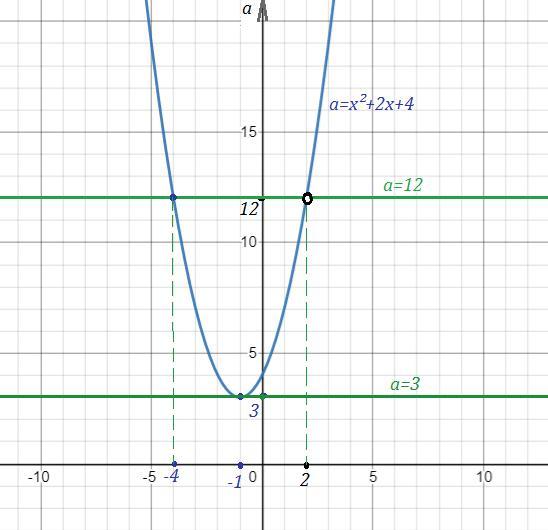
Квадратный трёхчлен имеет единственный корень, если дискриминант равен  0 .

$D=4(a-3)=0\ \ \ \Rightarrow \ \ \ \ a-3=0\ \ ,\ \ \boxed{a=3}$

При х=2 выражение   $x^2+2x+4$  принимает значение, равное 12 , так как  $2^2+2\cdot 2+4=4+4+4=12$ . Тогда параметр   а=12 .

При а=12 имеем  $x^2+2x+4=12\ \ ,\ \ x^2+2x-8=0\ \ \to \ \ x_1=-4\ ,\ x_2=2$ .

Так как  х=2 не входит в ОДЗ , то остаётся один корень х= -4 при  а=12 .

Наименьшее значение параметра "а" , при котором заданное уравнение имеет один корень - это а=3 .