найти площадь прямоугольной трапеции , если радиус круга , вписаного в нее, равен 12 см , а тупой угол трапеции равен 150 градусам
Ответы
Ответ дал:
1
Объяснение:
............ .......... . . ...
Приложения:
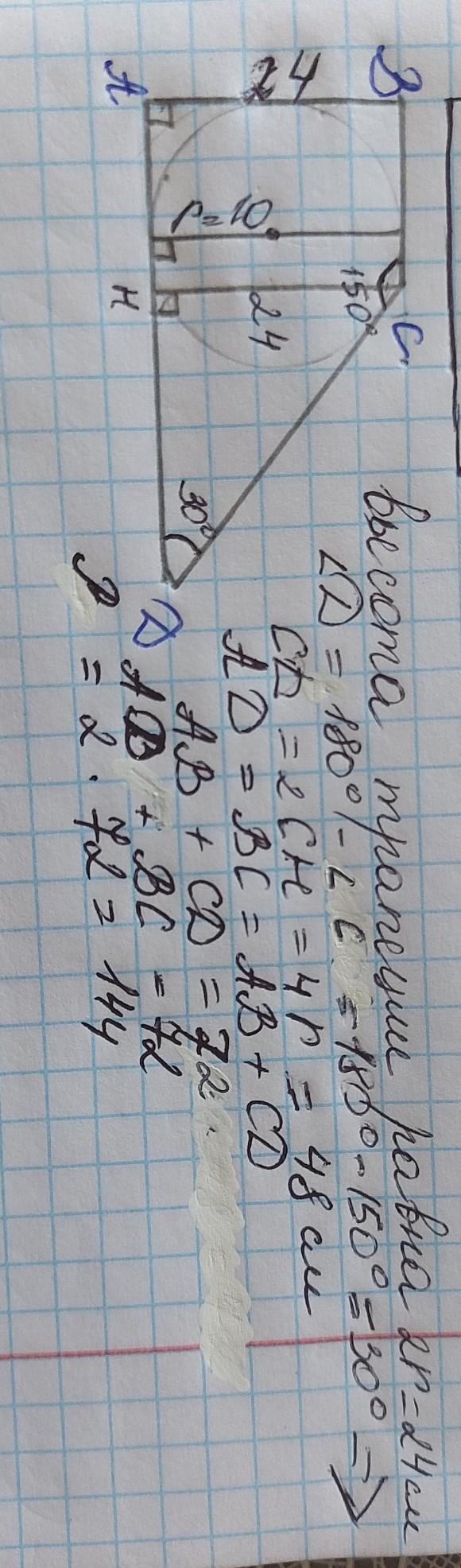
Ответ дал:
1
r= *h , откуда h = 24 см
острый угол трапеции равен 30° (360-90-90-150)
большая боковая сторона трапеции равна 48 см.
т.к. в трапецию вписана окружность, то по свойству суммы её боковых сторон и оснований равны.
сумма оснований = 24 см + 48 см = 72 см
Площадь трапеции = 1/2 * h * (a+b) = 1/2 * 24 * 72 = 864 см²
Ответ: 864 см²
Вас заинтересует
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад