Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
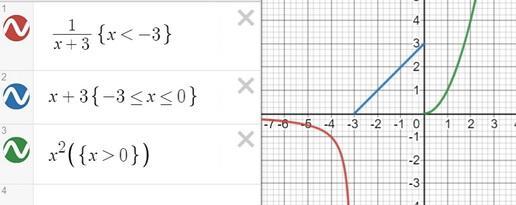
а)
точкa стыка промежутков x = -3
в точке х = -3 функция терпит разрыв. предел равен ∞, поэтому это точка разрыва II-го рода
исследуем поведение функции на отрезке (-3;0)
пределы существуют, на указанном промежутке функция непрерывна.
точка стыка промежутков x = 0
в точке х = 0 пределы существуют, но они разные, поэтому это точка разрыва I-го рода
смотрим поведение функции на отрезке (0;∞)
пределы существуют, функция непрерывна
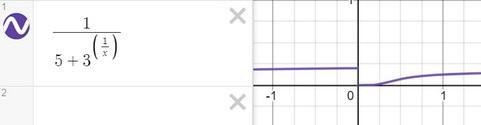
б)
для данной функции точка разрыва х = 0
исследуем ее
пределы существуют, но не равны, поэтому х = 0 точка разрыва I-го рода
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
