Question

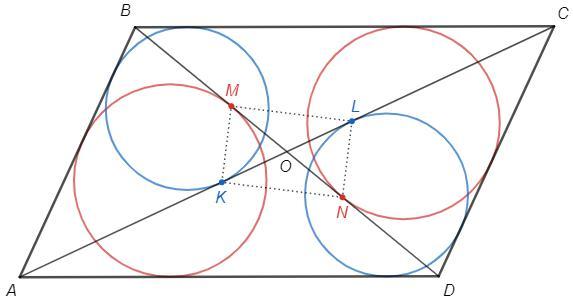
Дан параллелограмм ABCD. Окружности, вписанные в треугольники ABD и BDC, касаются диагонали BD в точках M и N соответственно. Окружности, вписанные в треугольники ABC и ADC,
касаются диагонали AC в точках K и L соответственно.
а) Докажите, что MKNL — прямоугольник.
б) Найдите площадь этого прямоугольника, если известно, что
BC − AB = 4, а угол между диагоналями параллелограмма ABCD
равен 30◦
.

Answer 1

a)

В треугольнике ABC

AK=p-BC, CK=p-AB

Пусть BC>AB, O - середина AC

OK =(CK-AK)/2 =(BC-AB)/2

Аналогично OM, OL, ON равны полуразности боковых сторон в соответствующих треугольниках.

AB=CD, BC=AD => OK=OL=OM=ON

MKNL - прямоугольник т.к. диагонали равны и точкой пересечения делятся пополам.

б)

KL=MN =2OK =BC-AB =4

S =1/2 *KL*MN *sin30 =4