Question

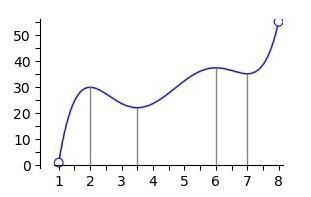
График функции на интервале (1,8). определите длину наибольшего промежутка, на котором производная отрицательна​

Answer 1

Ответ:

Пошаговое объяснение:

производная функции отрицательна там, где функция убывает

у нас функция убывает на отрезках [2; 3.5] и [6; 7]

наибольший отрезок будет [2;  3.5]

но на концах отрезка функция имеет локальный максимум и локальный минимум, поэтому в этих точках производная будет равна 0 и эти точки не могут быть включены в интервал, где производная отрицательна,

поэтому

наибольший промежуток, на котором производная отрицательна​, (2; 3,5)

а длина его d = 3.5 - 2 = 1.5