з вершини трикутника з основою а 60 проведено висоту h 12 і медіану m 13 знайти більшу бічну сторону
Ответы
Ответ дал:
2
Ответ:
Объяснение:
Решение дано на фото.
Приложения:
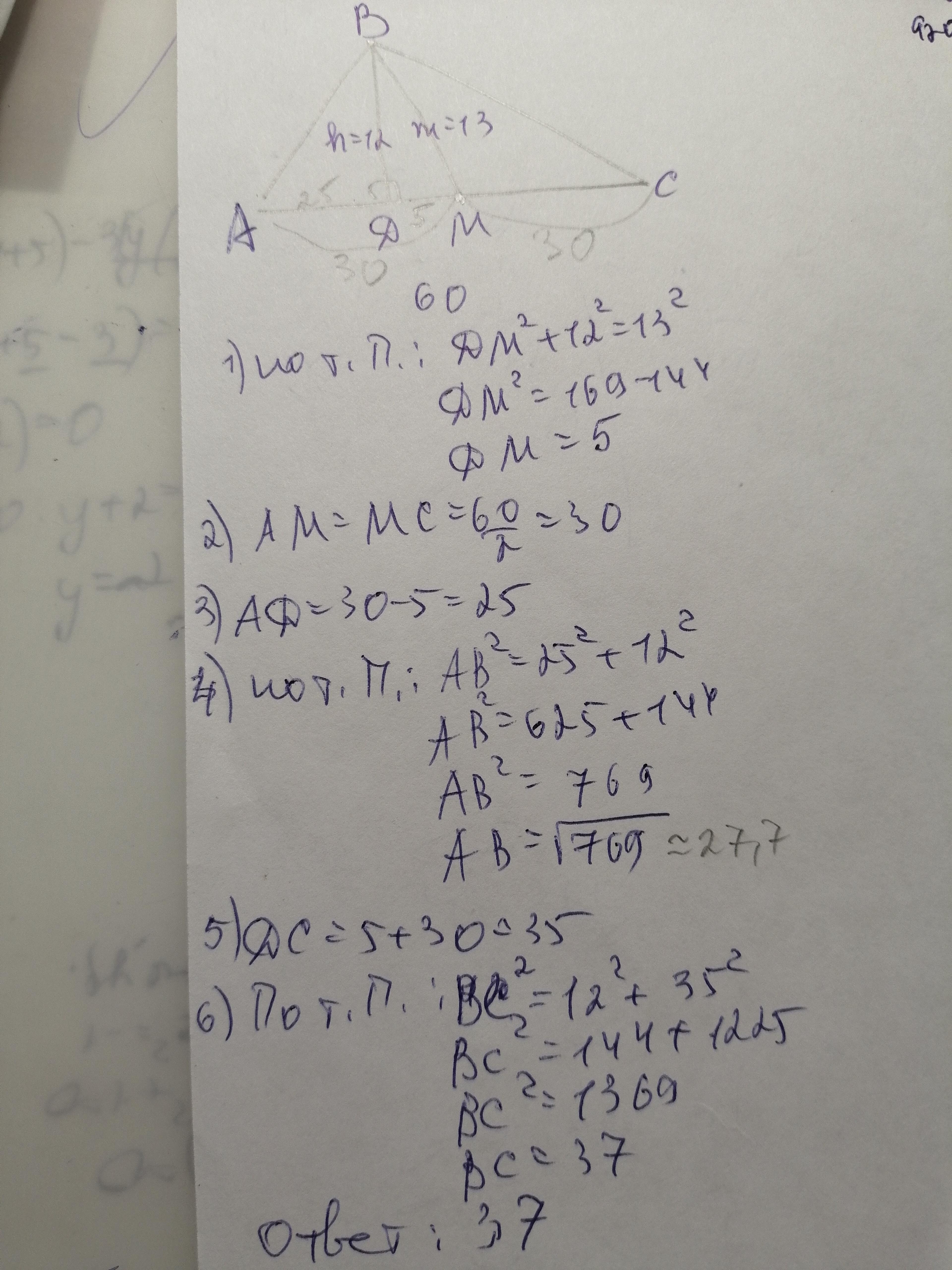
guffiii:
еп
Ответ дал:
1
Ответ:
37 см.
Объяснение:
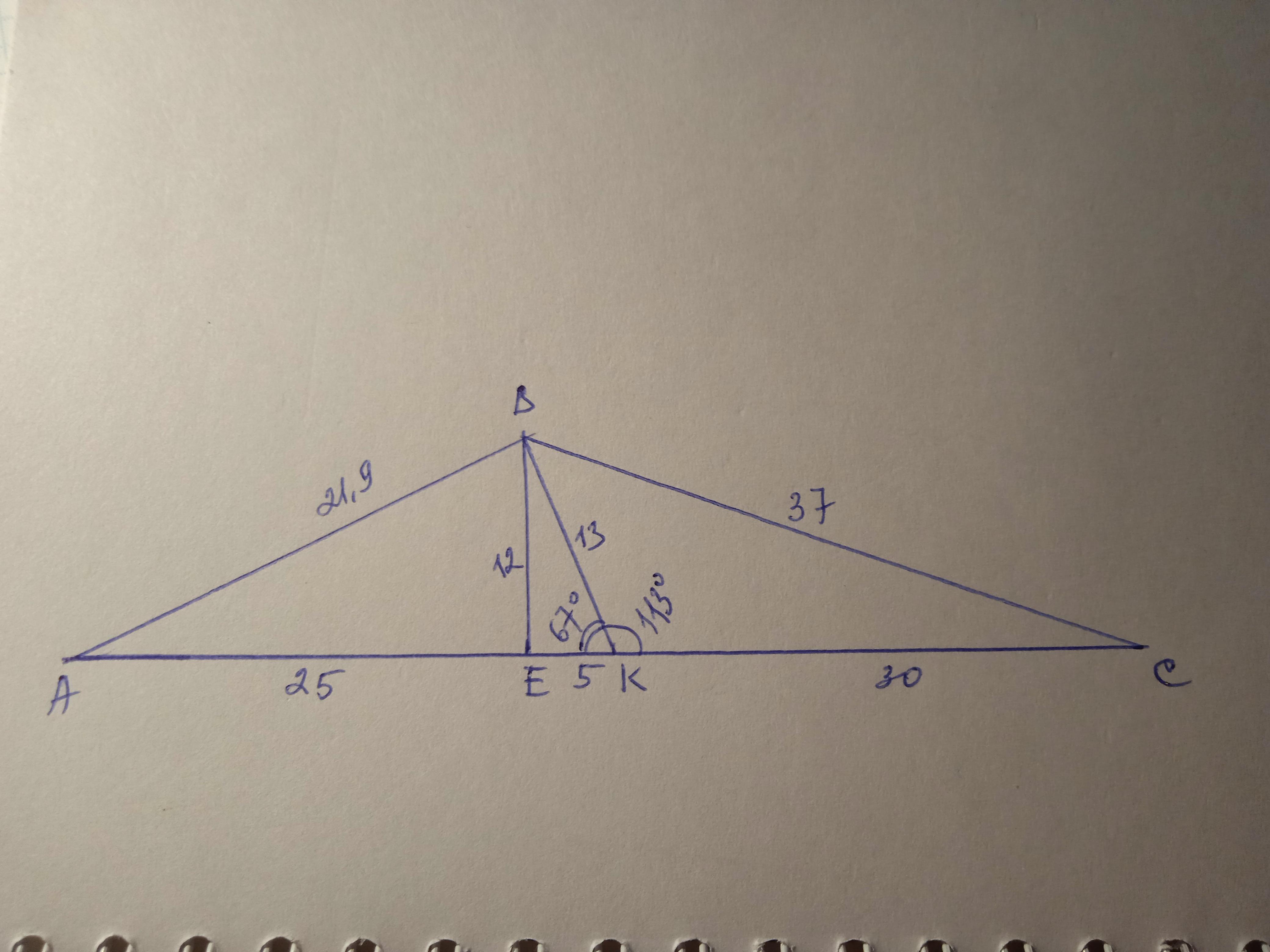
Дано: ΔАВС, ВЕ - висота, ВЕ=12 см, ВК - медіана, ВК=13 см, АС=30 см. Знайти ВС.
Розглянемо ΔВЕК - прямокутний, за теоремою Піфагора ЕК=5 см.
АК=СК=60:2=30 см за властивістю медіани
АЕ=АК-ЕК=30-5=25 см.
ΔАВЕ - прямокутний. За теоремою Піфагора АВ=21,9 см.
sin∠ВКЕ=12/13=0,923; ∠ВКЕ=67°
∠ВКС=180-67=113°
Знайдемо ВС за теоремою косинусыв:
ВС²=ВК²+КС²-2*ВК*КС*cos113°=169+900-2*13*30*(-0,39)=13732
ВС=√13732≈37 см.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад