В треугольнике ABC на стороне AB выбрали точку D и провели DE II BC (E - точка пересечения DE и AC). Общая хорда окружностей (ABE) и (ACD) пересекает BC в точке G. Доказать, что положение точки G не зависит от выбора точки D.
Для особо продвинутых - найти отношение BG/GC.
cos20093:
Я почти сразу обнаружил, что положение точки G именно такое, что (см. предыдущий комментарий) должно быть LM II BC. Поэтому я сосредоточился на том, чтобы это доказать, и не искал другие способы. Построение из красивого решения основано на том, что симедиана - ГМТ точек, расстояние от которых до сторон пропорционально этим сторонам. У биссектрисы все точки равноудалены от сторон, у медианы - обратно пропорционально удалены...
А упомянутый источник решения - англоязычный канал Michael Greenberg на ютубе.
понятно, может ответ все же напишите-для "истории" сайта?
вопрос могу создать, если нужно...симедиана-это что-то новое...
Ну как новенькое. Эмиль Лемуан в 1874 году представил работу, в которой доказал существование точки пересечение симедиан. А вообще это первое, что приводят в качестве примера применения теоремы Чевы - если точки на сторонах делят их в отношении F(a/b), F(b/c) F(c/a), где F(x) - любая функция, то чевианы пересекутся в одной точке.
Ну, и вводят еще понятие n-линий или n-чевиан. Скажем, медиана это 0-чевиана, F(x) = x^0; биссектриса - 1-чевиана F(x)=x (то есть основания биссектрис делят стороны пропорционально сторонам). Симедиана это 2-чевиана. F(x) = x^2; Она изогональна медиане, то есть симметрична относительно биссектрисы. Собственно, почти все, дальше есть куча красивых теорем. Точка их пересечения называется точкой Лемуана треугольника.
Уже в том, что я написал, есть что нужно доказывать. Скажем, если за определение принять "прямая, изогональная медиане", то надо еще доказать, что она делит сторону пропорционально квадрату отношения сторон. И это не так и просто, попробуйте. Подсказка - можно рассматривать площади.
наврал, F(a)/F(b), а не F(a/b).
Все комментарии пропадут, если не будет решения.
автор вопроса писать ответ не может, если у вас мальчишник-вот и пишите, если знаете что...
Ответы
Ответ дал:
2
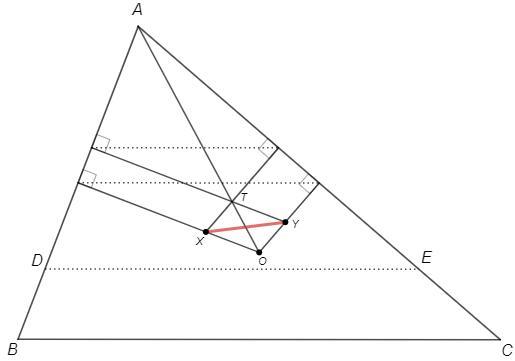
X, Y - центры окружностей ACD и ABE; O - центр окружности ABC
△XTO~△ABC (∠A =внешнему ∠T =∠X; проекции сторон XT и XO пропорциональны сторонам AB и AC)
Параллелограмм OXTY составлен из двух треугольников, подобных ABC => угол между его диагоналями, то есть между линией центров XY и AO не зависит от выбора точки D.
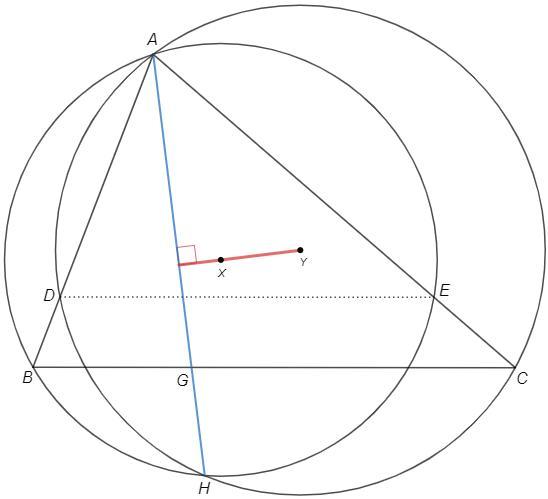
Общая хорда AH перпендикулярна линии центров => угол хорды AH и положение точки G не зависят от выбора точки D.
Пусть точки D и E совпадают в точке A.
Тогда окружности касаются сторон AB и AC.
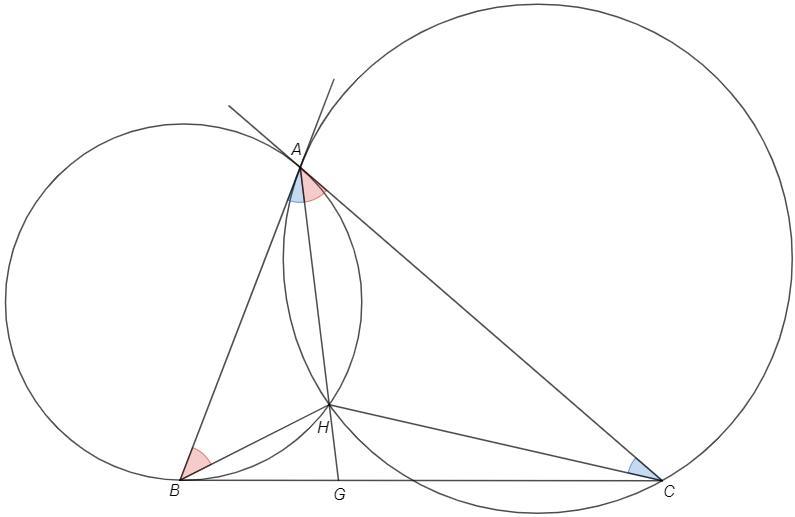
∠ABH=∠CAH, ∠ACH=∠BAH => △AHB~△CHA
высоты из H пропорциональны сторонам AB и AС
=> Н лежит на симедиане к основанию BC.
По свойству симедианы BG/GC =(AB/AC)^2
Приложения:
прикреплена статья Блинкова о симедиане
благодарю вас!
Очень красивое решение, и очень полезное по методу.
Спасибо за хорошую задачу
судя по двум окружностям, есть решение через поворотную гомотетию
например, треугольники BDH и ECH подобны по построению, A - центр поворотной гомотетии, H - неподвижная точка
но я в этом не силен
Вы по сути повторили сейчас решение, о котором я упоминал. Подобие этих треугольников уже означает, что это симедиана :) Высоты их - это расстояния до сторон. Я же говорил, что знаю очень простое и красивое решение, и даже упоминал его в комментарии, вместе со своим, использующем радикальную ось. А Вы сделали именно то, чего я хотел - предложили свой вариант решения :).
кстати, как сделать ответ "лучшим"? я не вижу соответствующей опции.
Должно быть 2 ответа, чтобы сделать ВЫБОР.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад