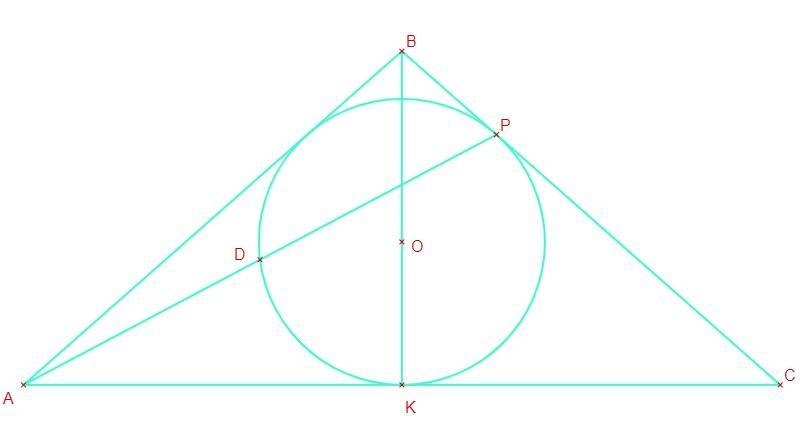
В равнобедренный треугольник ABC с основанием AC вписана окружность. Она касается стороны BC в точке P. Отрезок AP пересекает окружность точке D. Найдите площадь треугольника ABC, если известно, что AC =

, DP = 2.
Аноним:
5*sqrt(2)
Ответы
Ответ дал:
0
, так как точка K является серединой отрезка АС. Тогда
как касательные окружности.
По теореме о секущей и касательной:
По теореме Виета, получим .
Рассмотрим треугольник APC со сторонами AP = 4; PC =2√2 и AC = 4√2 и пусть ∠C = α. Используем теорему косинусов:
cos α = (a² + b² - c²)/2ab = ((4√2)² + (2√2)² - 4²)/[2*4√2*2√2] = 3/4
Из определения косинуса cos a = CK / BC отсюда BC = CK/cosa тогда получим BC = 2√2 / [3/4] = 8√2/3
По теореме Пифагора:
Искомая площадь треугольника кв. ед.
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад