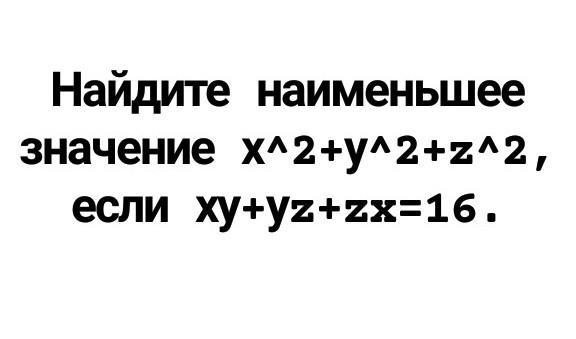Ответы
Ответ дал:
3
Идея решения подсказана теоремой Мюрхеда. Я не буду здесь говорить о ней, желающие сами могут ее найти (подчеркну только, что в теореме Мюрхеда говорится про неотрицательные числа, в нашем же случае это оказывается несущественным).
Обозначим A=x²+y²+z².
Удвоим первое выражение и вычтем из него удвоенное второе:
2A-32=2x²+2y²+2z²-2xy-2yz-2zx=(x²-2xy+y²)+(y²-2yz+z²)+(z²-2zx+x²)=
=(x-y)²+(y-z)²+(z-x)²≥0, причем равно нулю, если x=y=z. Поэтому минимальное значение A равно 16.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад