Помогите пожалуйста решить
Приложения:
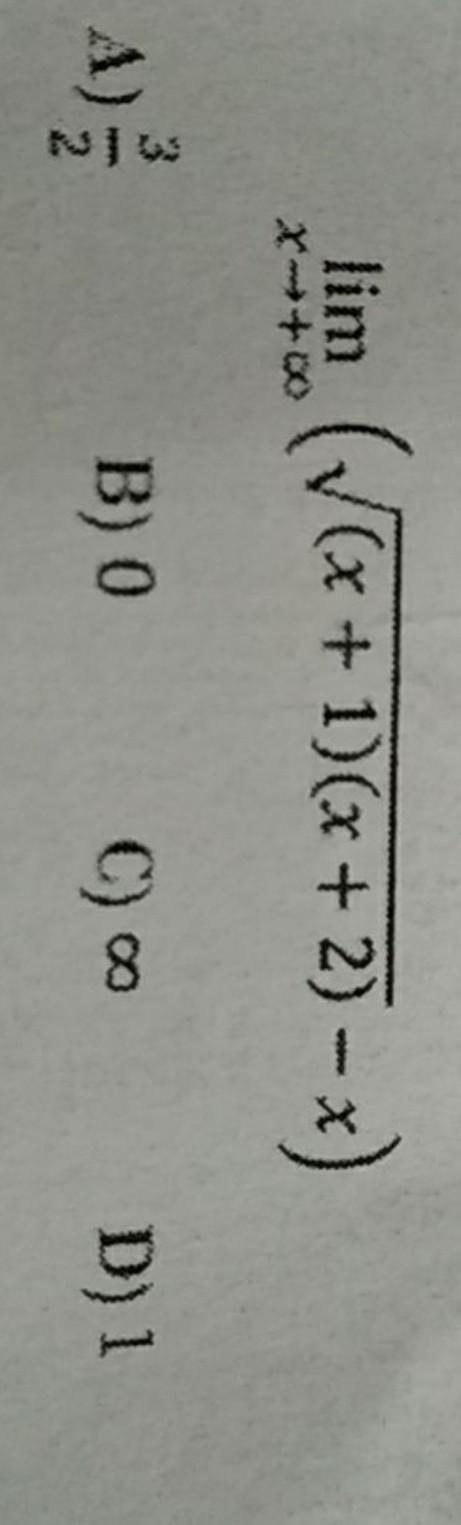
Аноним:
а можно решение
https://znanija.com/task/44729427
зачем спамите ?
больше не повторится, было срочно....
ваш спам-ответ удален. помогу если поможете другим (у вас сейчас минус 30 балов)
даже минус 35
хорошо обязательно помогу , а вы сейчас ответе пожалуйста, ....
обязательно отвечу, вначале помогите другим !!!
вот помог я
помогла *
Ответы
Ответ дал:
1
Ответ:
3/2
Объяснение:
во вложении
Приложения:

и я успел, через 4 минуты зазвенит будильник и я проснусь )
а можно я отвечу другим а вы мне каждый день
помогите пожалуйста, у меня в вопросах есть одна задача где нужно найти площадь фигуры
помогите пожалуйста
у вас все решено
помогите пожалуйста
там у вас не все в порядке с условием
помогите
помогите пожалуйста
помогите пожалуйста решить
Ответ дал:
2
Ответ.
спасибо большое
можно и кнопочку "спасибо" нажать
давайте друг друга поблагодарим )
давайте )
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад