Question

Помогите пожалуйста!!!!
Окружность, вписанная в прямоугольный треугольник ABC, касается катета AC в точке K. Найдите радиус окружности, описанной около треугольника ABC, если AK=2, KC=4.

Answer 1

Ответ:

5 ед.

Пошаговое объяснение:

Окружность вписана в треугольник АВС.

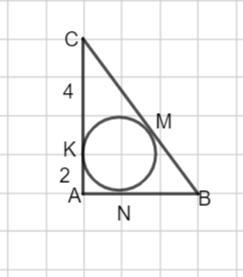
К - точка касания катета АС, М - точка касания гипотенузы ВС, точка N  - точка касания катета АВ.

АК=2, КС=4. Тогда катет АС= 4+2=6

По свойству отрезков касательных

СМ=СК=4, КА=KN=2.

Пусть BN=BM=x. Тогда гипотенуза ВС=4 + x, а катет АВ= x + 2.

Составим уравнение, применяя теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$BC^{2} =AC^{2} +AB^{2} ;\\(4+x)^{2} =6^{2} +(2+x)^{2} ;\\16+8x+x^{2} =36+4+4x+x^{2} ;\\8x-4x=40-16;\\4x=24;\\x=24:4;\\x=6$

Тогда гипотенуза ВС=4+6=10.

Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы.

$R=\dfrac{c}{2} ;\\\\R=\dfrac{10}{2}=5$