Question

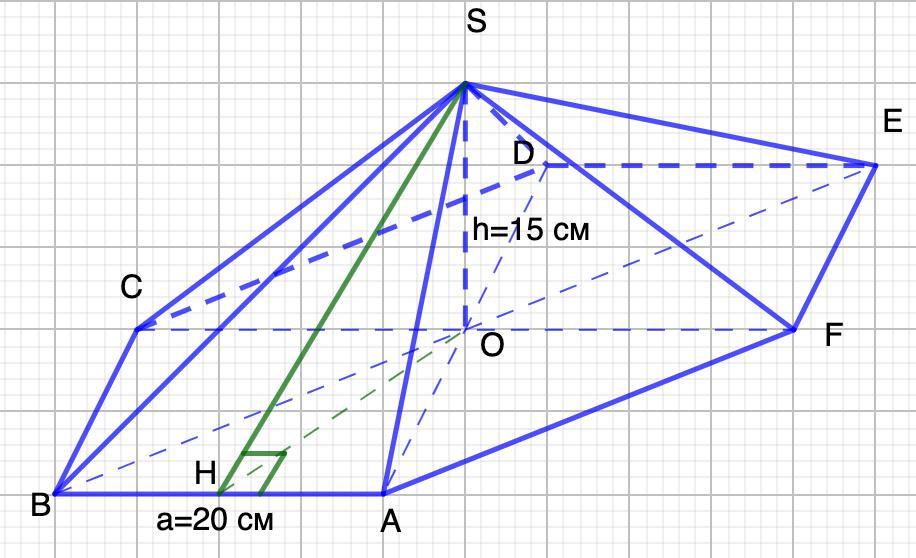
Задана правильная шестиугольная пирамида, высота которой равна 15 см, а сторона основания – 20 см.
а) Определите длину бокового ребра пирамиды;
б) Определите длину апофемы;
в) Определите площадь боковой поверхности пирамиды.
с чертежом

Answer 1

Ответ:

$1)\;\;\;AS=25cm\\2)\;\;\;SH=5\sqrt{21}cm\\3)\;\;\;S_{bok}=300\sqrt{21} cm^2$

Объяснение:

Дано: Правильная шестиугольная пирамида SABCDEF.

SO=15 см - высота

ВА=20 см - сторона основания

Найти:

Боковое ребро AS; апофему SH, площадь боковой поверхности.

Решение:

Правильная шестиугольная пирамида имеет в основании правильный шестиугольник. Боковые грани - равнобедренные треугольники.

1. Рассмотрим ΔВОА - равносторонний (свойство правильного шестиугольника)

⇒ОА=20 см.

2. Рассмотрим ΔASO - прямоугольный (SO - высота)

По т. Пифагора:

$AS=\sqrt{SO^2+AO^2}=\sqrt{225+400}=25\;(cm)$

3. Рассмотрим ΔASB - равнобедренный.

⇒SH - высота, медиана.

⇒ВН=AH=10 см

4. Рассмотрим ΔHSA - прямоугольный.

По т. Пифагора:

$SH=\sqrt{SA^2-AH^2}=\sqrt{625-100}=\sqrt{525}=5\sqrt{21}\;(cm)$

5. Площадь боковой поверхности равна площади 6 граней.

Найдем сначала площадь одной грани, а затем шести:

$S=\frac{1}{2}*BA*SH=\frac{1}{2}*20*5\sqrt{21}=50\sqrt{21}\;(cm^2)\\S_{bok}=50\sqrt{21}*6=300\sqrt{21}\;(cm^2)$