В квадрат вписаны две окружности. Первая окружность радиусом 2.25 касается двух сторон квадрата, вторая окружность радиусом 3.75 касается двух остальных сторон и первой окружности. Найдите площадь квадрата.
Мартын05:
104,9 (округлённо)
точнее: 54+36√2
я почти "в уме" считал :)
а почему сразу не написать что диагональ равна d = 6(1 + √2)? У вас рисунок просит буквально :) Площадь равна S = d^2/2 = 36(3+2√2)/2;...
действительно... не увидела)) про два квадрата в углах написала, а общую диагональ... не увидела... куда смотрела ?! видимо, терзало сомнение: вдруг это ломаная)) про углы не подумала
Ответы
Ответ дал:
2
Ответ: 54+36√2
Объяснение:
Отрезки касательных, проведенных к окружности из одной точки, равны.
или Окружность, вписанная в прямой угол, высекает квадрат со стороной, равной радиусу...
на рисунке можно найти еще один (получившийся) квадрат (ABCD) с известной диагональю...
Приложения:
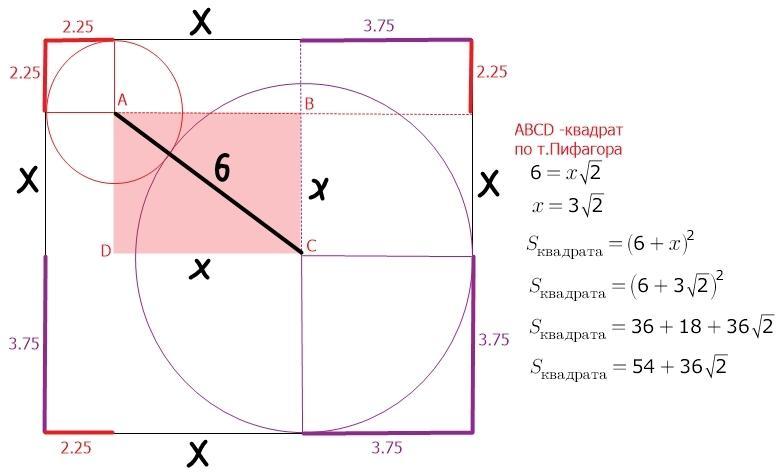
ABCD -квадрат? На рисунке - это скорее всего прямоугольник. АВ не равно ВС.
Посмотрите на окружность радиуса 3,75. Радиус окружности меньше DC, но больше BC. Следовательно ABCD - не квадрат.
так это рисунок, а не чертеж... здесь и соотношение радиусов не выдержано... и окружности без циркуля (на глаз) построены... и длина АС совсем не шесть (чего ? см ? км ?)
и фигура со сторонами 3.75 тоже не похожа на квадрат...
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад