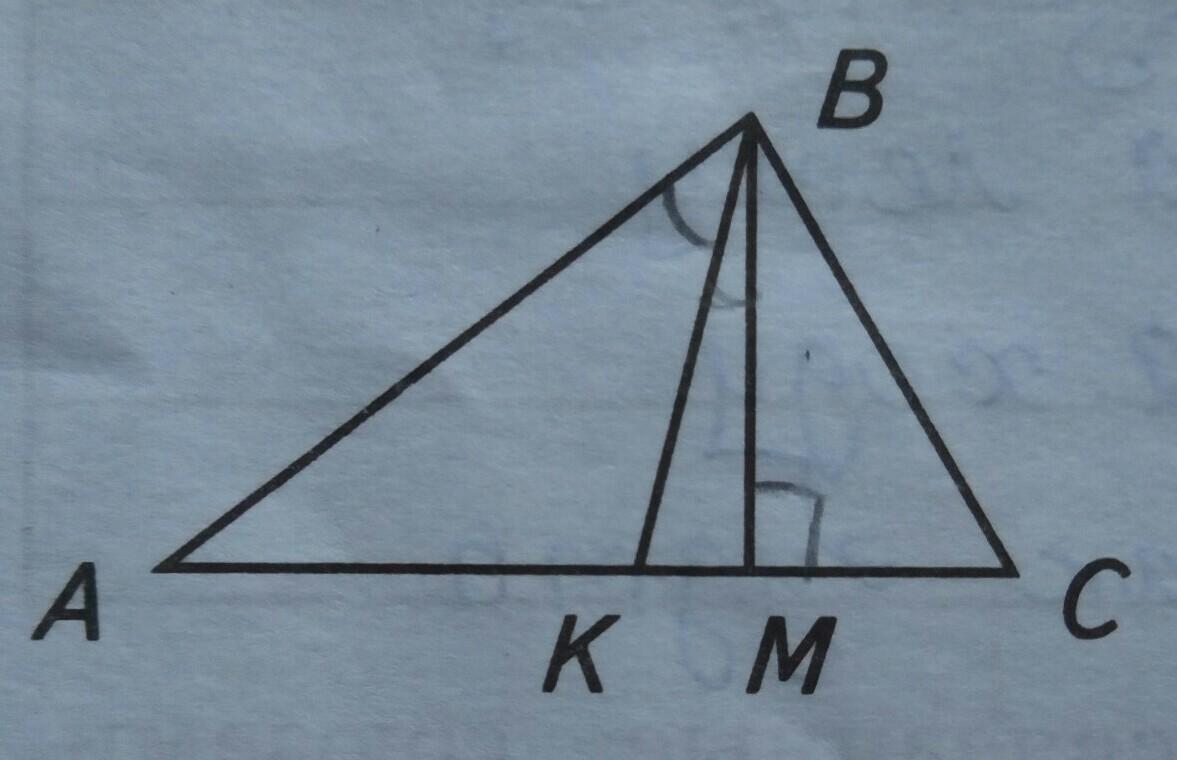
В треугольнике ABC проведена биссектриса bk и высота bm, угол ABC = 80°, угол BCA = 60°. Найди угол Kbm между биссектрисой и высотой.
Приложения:
Ответы
Ответ дал:
2
Ответ:
10
Объяснение:
рассмотрим треугольник bmc. угол bmc=90 (тк bm высота), угол bca=60 (по условию), следовательно угол cbm=180-(90+60)=30
угол cbk=угол abc/2 (тк bk биссектриса). cbk=80/2=40
угол kbm=угол cbk - угол cbm = 40-30=10
cathappy129:
Благодарю!
Ответ дал:
0
Ответ:
10°
Объяснение:
уг ABK= уг CBK=80:2=40°
уг BMC=90° т.к. BK высота
уг MBC=180-(90+60)=30°
↓↓
уг KBM=40-30=10°
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад