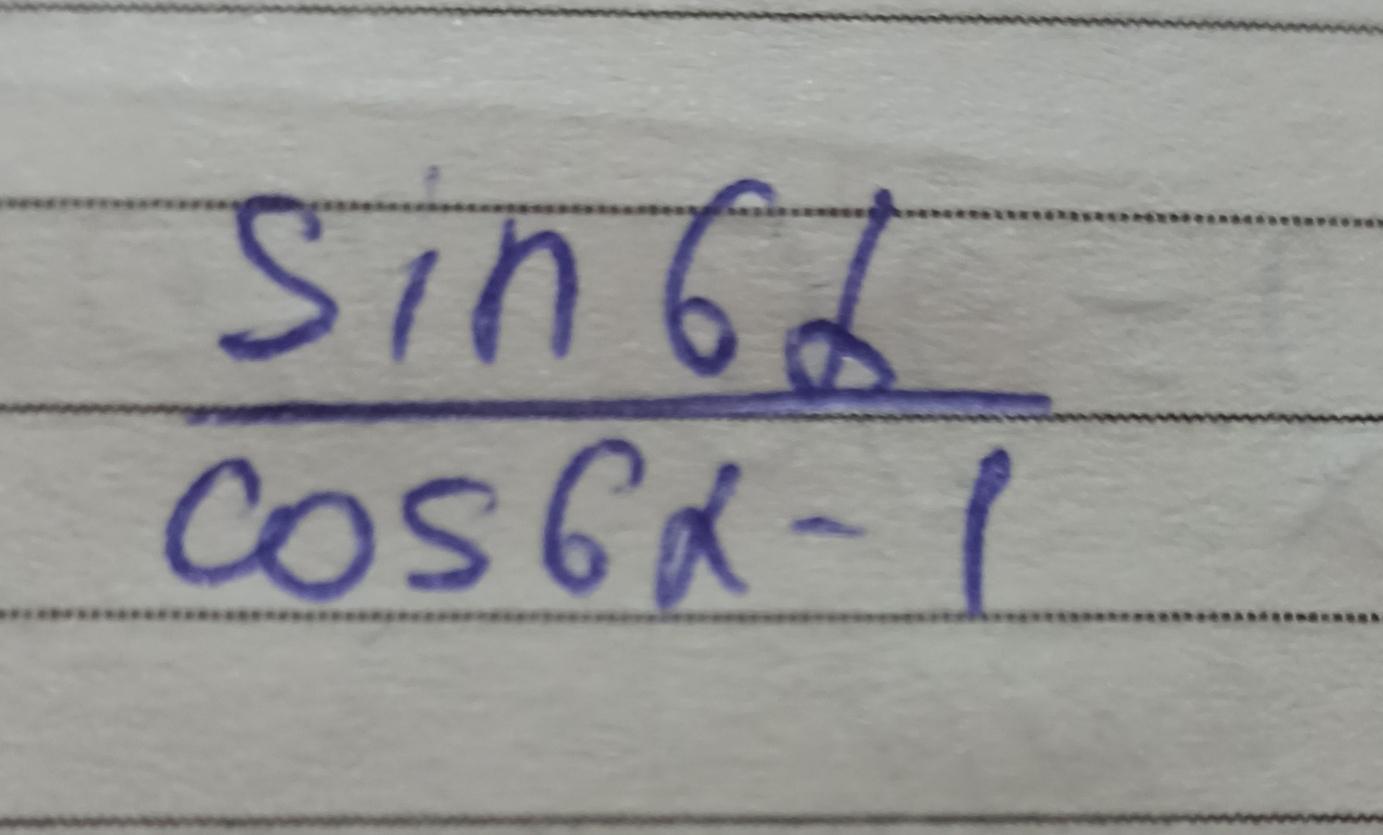Ответы
Ответ дал:
2
Объяснение:
Можно и преобразовать дальше, если необходимо:
Ответ дал:
0
Ответ: - ctg3α .
Объяснение:
sin6α/(cos6α - 1) = sin( 2*3α)/( cos( 2*3α ) - 1 ) = 2sin3αcos3α/(cos²3α - -sin²3α -1 ) = 2sin3αcos3α/[- ( 1 - cos²3α ) - sin²3α ] = 2sin3αcos3α/(- sin²3α -
- sin²3α ) = 2sin3αcos3α/(- 2sin²3α ) = - cos3α/sin3α = - ctg3α .
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад