Question

Основанием пирамиды, вписанной в конус, служит четырехугольник, у которого смежные стороны попарно равны, а угол между одной парой смежных сторон равен α. Найти отношение объема пирамиды к объему конуса.

Answer 1

Ответ:

$\frac{V_p}{V_k} =\frac{2\sin(\alpha )}{\pi }$

Объяснение:

Объём пирамиды равен

$V_p=\frac{1}{3} S_{o}h$

объём конуса

$V_k=\frac{1}{3} \pi R^{2}h$

Их отношение будет равно

$\frac{V_p}{V_k} =\frac{S_o}{\pi r^{2} }$

То есть отношение площадей

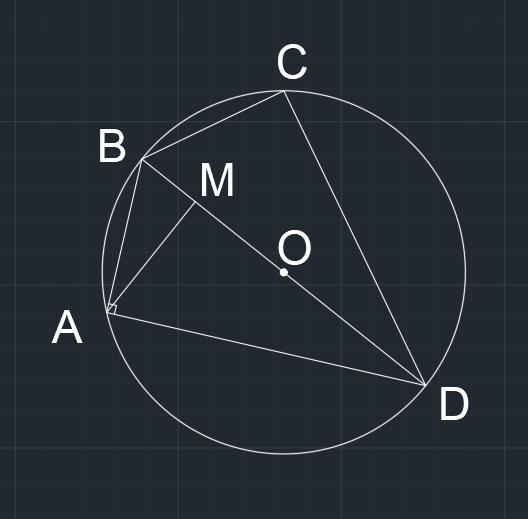
На рисунке представлено основание.

AB=BC и CD=DA

Угол между AB и BC равен α

Прямая DB будет проходить через центр окружности и являться диаметром, поскольку одновременно является биссектрисой углов ABC и CDA.

То есть DB = 2r

Треугольник ABD будет прямоугольным с прямым углом A, поскольку он опирается на дугу в 180 градусов.

ABD = α/2 заменим для простоты на β

Тогда

$AB=BD\cos(\beta )=2r\cos(\beta ); \\AD=BD\cos(\frac{\pi }{2} - \beta )=BD\sin(\beta)=2r\sin(\beta)$

Площадь треугольника будет

$S_{ABD} =\frac{1}{2} AB*AD=\frac{2r\cos(\beta)*2r\sin(\beta)}{2} =r^{2} 2\cos(\beta)\sin(\beta) =r^{2} \sin(2\beta )=r^{2} \sin(\alpha )$

Площадь основания равна двум таким площадям, итого получаем

$\frac{V_p}{V_k} =\frac{2S_{ABD}}{\pi r^{2} }=\frac{2r^{2} \sin(\alpha )}{\pi r^{2} }=\frac{2\sin(\alpha )}{\pi }$