Ответы
Ответ дал:
0
Ответ:
2
Пошаговое объяснение:
Решаем методом интервалов - на числовой прямой отмечаем нули: 1, 3 и 4, расставляем знаки на интервалах, не забывая выколоть 1 и 3 и из-за квадрата в числителе знаки интервалов рядом с точкой 4 не чередуется. Решением неравенства является x∈(1;3)∪{4}, откуда мы понимаем, что целых решений всего 2: 2 и 4
palilov243659:
(x-4)^2-кратный корень х=4
кроме того, 1 и 3 не входят в ОДЗ
исправил всё
Ответ дал:
1
Ответ:
2
Пошаговое объяснение:
///////////////////////
Приложения:
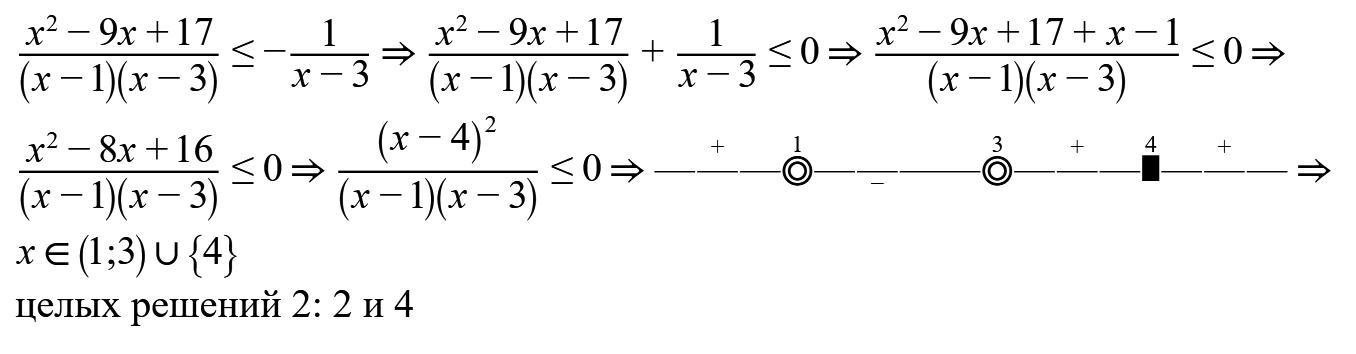
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
9 лет назад
