Ответы
Ответ дал:
0
Решение:
2sin^3x-cos2x-sinx=0
sinx(2sin^2x-1)-cos2x=0
-sinxcos2x-cos2x=0
-cos2x(sinx+1)=0
cos2x=0
2x=п/2(2k+1)
x=п/4(2k+1)
sinx=-1
x=-П/2+2пk
2sin^3x-cos2x-sinx=0
sinx(2sin^2x-1)-cos2x=0
-sinxcos2x-cos2x=0
-cos2x(sinx+1)=0
cos2x=0
2x=п/2(2k+1)
x=п/4(2k+1)
sinx=-1
x=-П/2+2пk
Ответ дал:
0
//////////////////////////////////////////////////////////////////
Приложения:
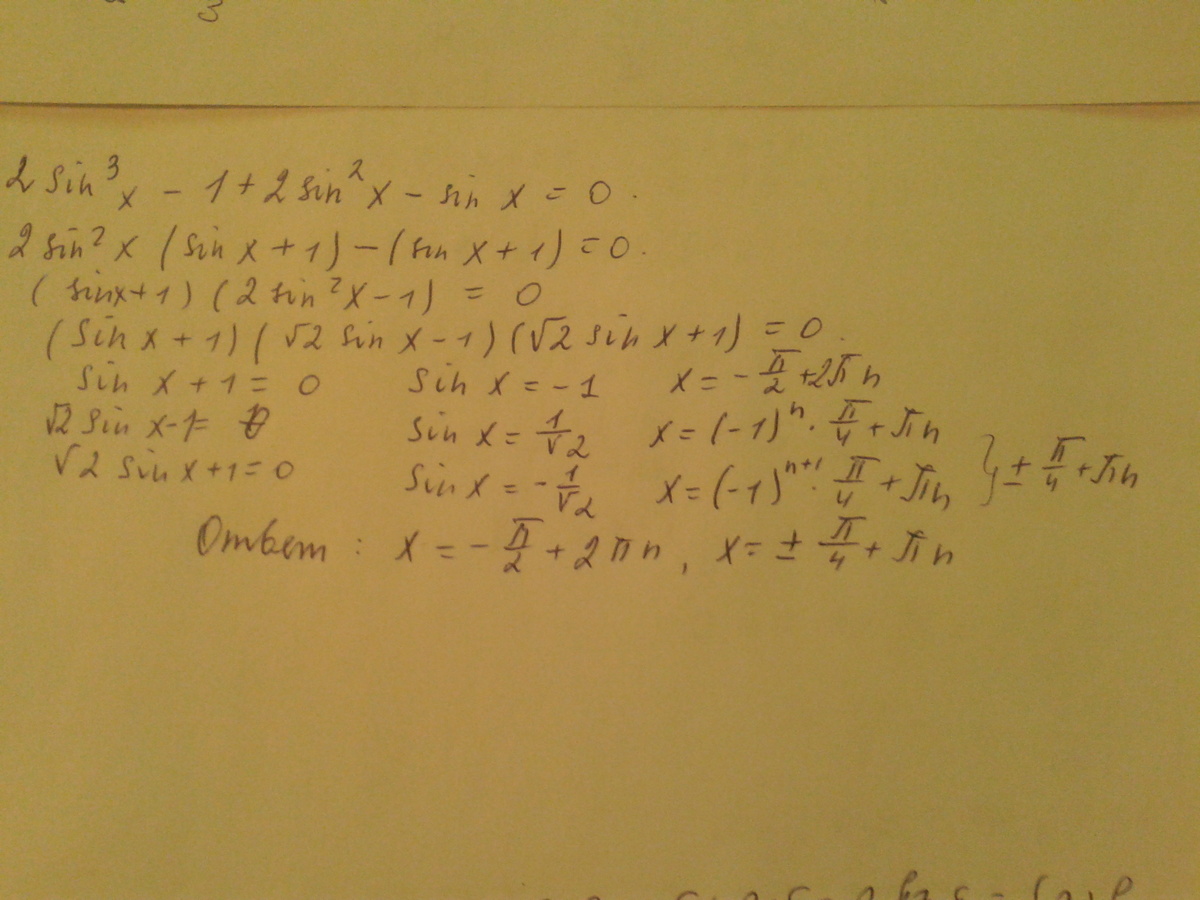
Вас заинтересует
8 лет назад
8 лет назад
10 лет назад
10 лет назад