Question

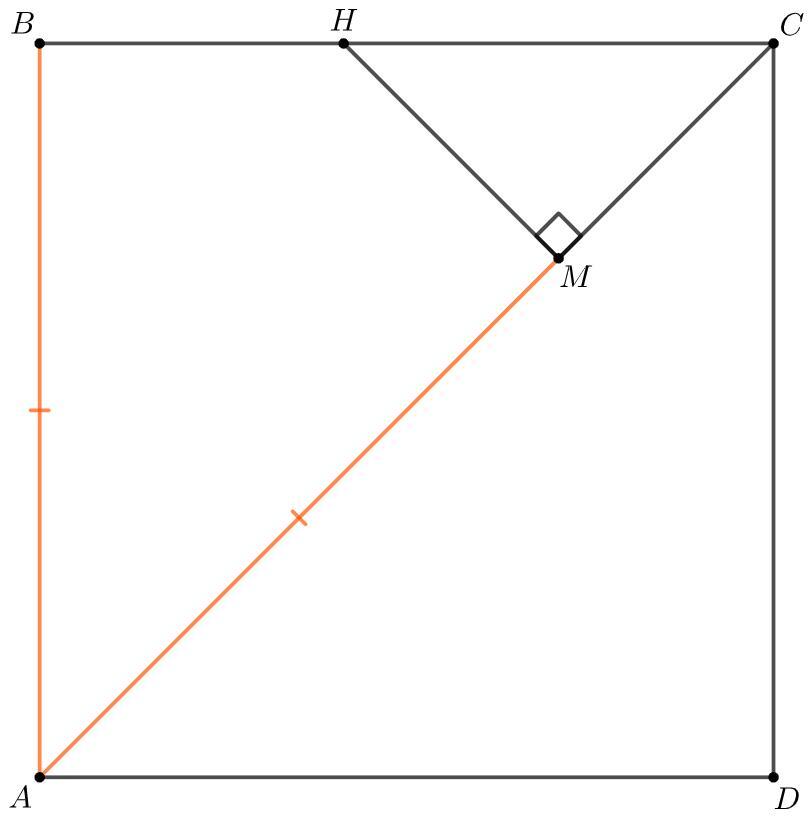
На диагонали AC квадрата ABCD выбрали такую точку M, что AB=AM. Перпендикуляр к отрезку AC в точке M пересекает сторону BC в точке H. Докажите, что BH=k*MC. В ответ запишите значение k.

Answer 1

Ответ: 1

Объяснение:

Пусть $AB=1$, тогда

По т. Пифагора $AC=\sqrt{AB^2+BC^2}=\sqrt2$

$MC=AC-AM=\sqrt2-1$

$HC=MC:\cos \angle ACB=\dfrac{\sqrt2-1}{1/\sqrt2}=2-\sqrt2$

$BH=BC-HC=1-2+\sqrt2=\sqrt2-1$

$k=\dfrac{BH}{MC}=\dfrac{\sqrt2-1}{\sqrt2-1}=1$