Question

даю 50 баллов!!!!
Отрезки, соединяющие вершины треугольника с точками касания вневписанных окружностей треугольника со сторонами, пересекаются в одной точке. Эта точка называется точкой Нагеля.


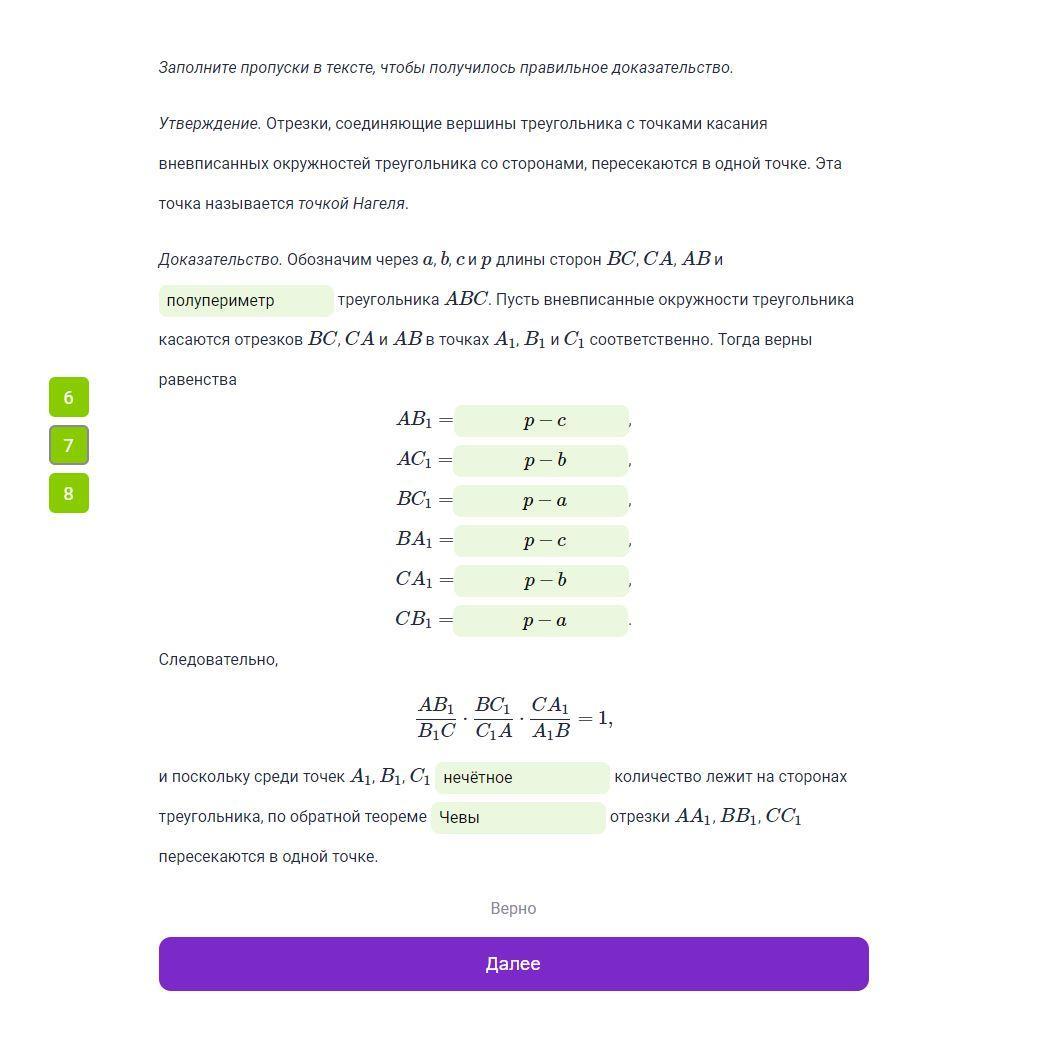
Доказательство. Обозначим через a, b, c и p длины сторон BC, CA, AB и

полупериметр

треугольника ABC. Пусть вневписанные окружности треугольника касаются отрезков BC, CA и AB в точках A1, B1 и C1 соответственно. Тогда верны равенства

AB1=______

AC1=______

BC1=_____

BA1=______

CA1=__________

CB1=______

Следовательно,

AB1B1C⋅BC1C1A⋅CA1A1B=1,

и поскольку среди точек A1, B1, C1 ________ количество лежит на сторонах треугольника, по обратной теореме _______ отрезки AA1, BB1, CC1 пересекаются в одной точке.

Answer 1

Ответ: лови

Объяснение: