Найдите диагонали равнобокой трапеции, если её меньшее основание равно 7 см, боковая сторона равна 8 см, а один из углов равен 120°.
Аноним:
Теорема косинусов.
Спасибо
Пожалуйста.
Ответы
Ответ дал:
1
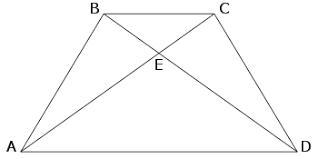
Диагонали равнобедренной трапеции равны. На рисунке ВС = 7 см, AB = CD = 8 см, угол АВС = 120°. Рассмотрим треугольник АВС. Его сторона АС одновременно является его диагональю. По теореме косинусов: АС² = АВ²+ВС²-2АВ*ВС*cos120°
АС² = 49+64-2*7*8*cos120°
АС² = 113-112*(-0,5)
АС² = 113+56
АС² = 169
АС = 13
Итак, диагонали трапеции равны по 13 см.
Ответ: 13 см; 13 см.
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад