Помогите, пожалуйста.
Приложения:
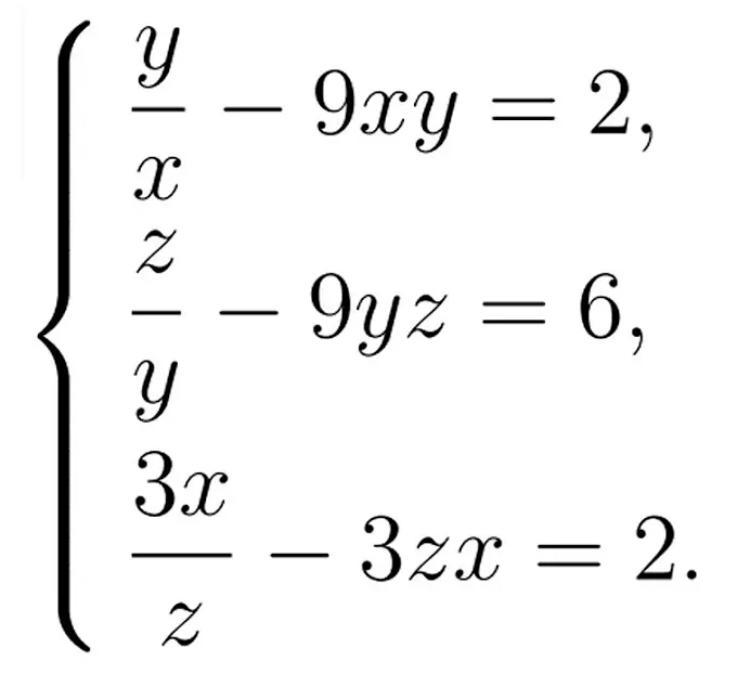
armen1549:
С объяснением
Через тригонометрическую замену попробуйте
Решал двумя разными способами. Ответ один и тот же- нет решения. Или я ошибаюсь?
Ответ такой должен получиться https://ibb.co/ZN1rZMT
понял ошибку
Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
3x=tga, 3y=tgb, z=tgc, a,b,c∈(-π/2; π/2)
tgb/tga-tgbtga=2⇒tgb=2tga/(1-tg²a)=tg2a⇒b=2a+kπ⇒3y=tg2a
tgc/tgb-tgctgb=2⇒tgc=2tgb/(1-tg²b)=tg2b⇒c=2b+nπ⇒z=tg4a
tga/tgc-tgatgc=2⇒tga=2tgc/(1-tg²c)=tg2c⇒a=2c+mπ
Так как a,b,c∈(-π/2; π/2), то m,n,k=±1
a=2c±π
b=2a±π
c=2b±π
a=2c±π=2(2b±π)±π=2(2(2a±π)±π)±π=8a±4π±2π±π
a={±π/7; ±3π/7; ±5π/7; ±π}
Но x≠0⇒a≠ ±π⇒a={±π/7; ±3π/7; ±5π/7}
Проверяя полученные ответы и учитывая ограничения введённые для а имеем
3x=tga, 3y=tg2a, z=tg4a, a={±π/7; ±2π/7; ±3π/7}
x=(1/3)tga, y=(1/3)tg2a, z=tg4a, a={±π/7; ±2π/7; ±3π/7}
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад