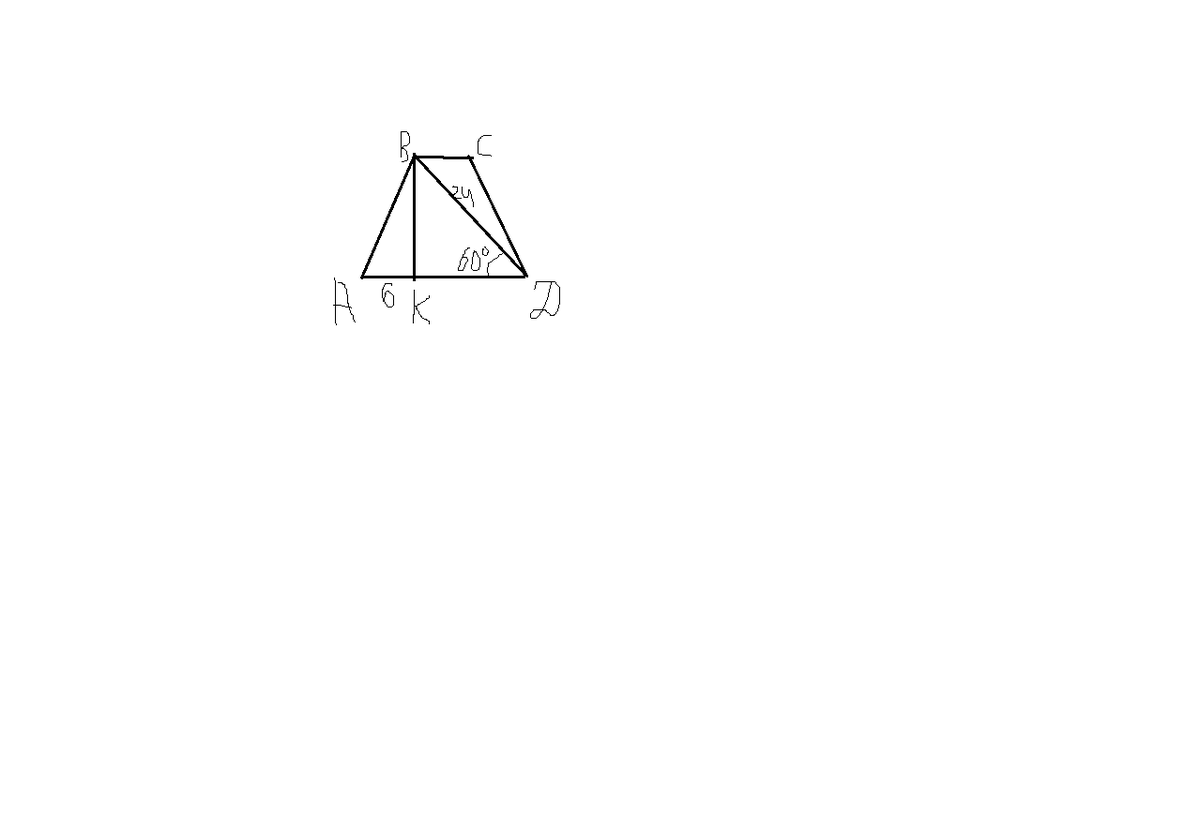
Вычислите площадь равнобедренной трапеции, в которой диагональ образует с большим основанием угол 60 гр. BD=24, AK=6, угол BDK=60 гр.
Приложения:
Ответы
Ответ дал:
0
Можно без рисунка?
В прямоугольном треугольнике КВD против угла 30° лежит катет КD, равный половине гипотенузы BD, то есть KD=12. Тогда второй катет ВК (он же высота трапеции) равен ВК=√(BD²-KD²) = √(576-144) = √432 = 12√3.
В равнобокой трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований. Значит KD= полусумме оснований. Тогда площадь трапеции, которая равна произведению полусуммы оснований на высоту, равна:
Sabcd = KD*BK = 12*12√3 = 144√3.
В прямоугольном треугольнике КВD против угла 30° лежит катет КD, равный половине гипотенузы BD, то есть KD=12. Тогда второй катет ВК (он же высота трапеции) равен ВК=√(BD²-KD²) = √(576-144) = √432 = 12√3.
В равнобокой трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований. Значит KD= полусумме оснований. Тогда площадь трапеции, которая равна произведению полусуммы оснований на высоту, равна:
Sabcd = KD*BK = 12*12√3 = 144√3.
Ответ дал:
0
У меня точно так же получилось)
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад