Question

найдите наибольшее и наименьшее значения функции f(х)=х^3-3х^(2)-12х на отрезке -3;4

Answer 1

Ответ:

Объяснение:

воспользуемся производной первого порядка

f'(x) = 3x²-6x-12

теперь критические точки

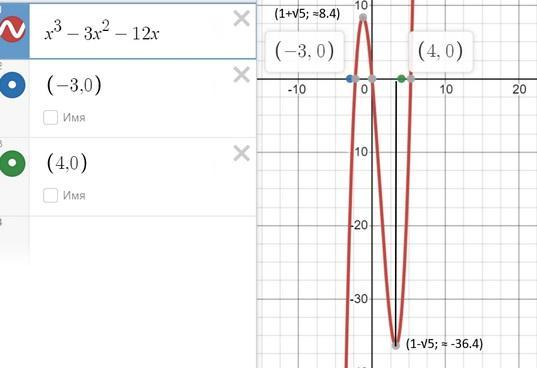
3x²-6x-12 = 0  ⇒ x₁ = 1+√5≈ 3.2   x₂=1-√5≈ -1.2  обе точки попадают в нужный отрезок

считаем значение функции в критических точках и на концах отрезка

f(1+√5) ≈ -36.4

f(1-√5) ≈ 8.4

f(-3) = -18

f(4) = -32

ответ

fmin = f(1+√5)  ≈ -36.4, fmax =f(1-√5) ≈ 8.4