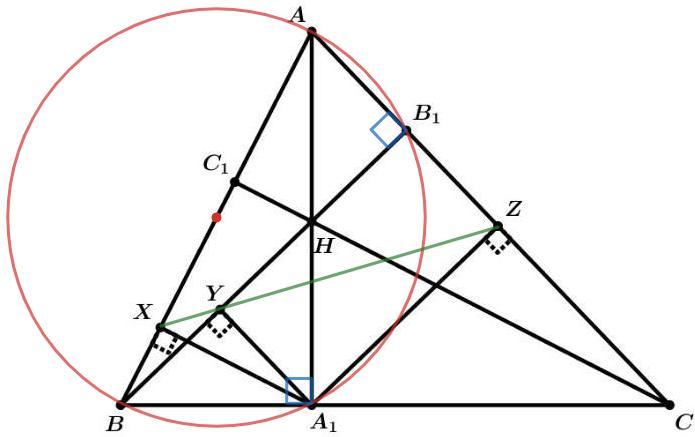
Пусть AA1, BB1, CC1 — высоты остроугольного треугольника ABC, пересекающиеся в точке H. Точки X, Y, Z — основания перпендикуляров из точки A1 на прямые AB, BB1, AC соответственно. Выберите 4 точки: 3 вершины треугольника и точку, лежащую на описанной окружности этого треугольника, такие, что на картинке есть 3 точки, лежащие на прямой Симсона выбранной точки относительно выбранного треугольника
orjabinina:
такая задача была. Поищите в поиске
И где чертеж?
А , это был Ваш вопрос и Вам косинус отвечал.
Ответы
Ответ дал:
4
AA1, BB1 - высоты => AA1B=AB1B=90
Отрезок AB виден из точек A1 и B1 под прямым углом - точки A1 и B1 лежат на окружности c диаметром AB.
То есть точка A1 лежит на описанной окружности треугольника ABB1.
Тогда основания перпендикуляров из A1 к сторонам треугольника ABB1 лежат на прямой Симсона (X-Y-Z).
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад