Предмет: Геометрия
Автор: vlad8748
Вопрос задан 7 лет назад

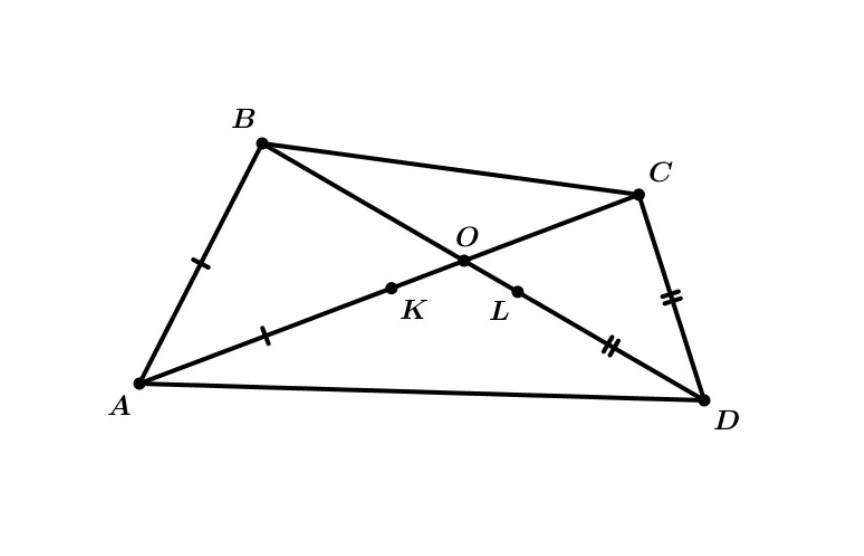
Диагонали вписанного четырёхугольника ABCD пересекаются в точке O. На его диагоналях AC и BD отметили точки K и L соответственно так, что AK=AB и DL=DC. Выберите все гарантированно верные утверждения.
Прямые AD и BC антипараллельны относительно угла AOD
Прямые AD и BC антипараллельны относительно угла ACD ∠BKA=∠CLD Прямые BC и KL параллельны
Прямые BC и KL антипараллельны относительно угла BOC
Прямые AD и KL параллельны

Приложения:

Матов: AD || KL это всегда, так как ABCD вписанный, значит KAB=CDO, ABD=ACD но так как AB=AK, CD=OD тогда ABK=DCL = (180-KAB)/2 откуда KBO = LCO = ACD-DCL то есть треугольники BKO, CLO подобны откуда OK/OL = OB/OC = AB/CD = AK/LD по теореме Фалеса KL || AD

cos20093: можно так OK/OL = OB/OC = AO/DO, так как AOD и BOC подобны. Очень красивая задачка.

cos20093: Матов avatar
А почему Вы не выкладываете решение? По-моему, стоит :)

Матов: Здравствуйте, может лучше вы?

cos20093: Как это я буду Ваше решение выкладывать? У Вас красивая цепочка рассуждений, мне кажется, это стоит публикации.

cos20093: Я бы вообще рассуждал по другому. ABK и DCL равнобедренные, с одинаковыми углами при вершине => они подобны => равны внешние углы BLC и CKB => BKLC вписанный => KL антипараллельна BC относительно диагоналей AC и BD => KL II AD, так как обе прямые антипраллельны BC отностительно одной и той же пары прямых.