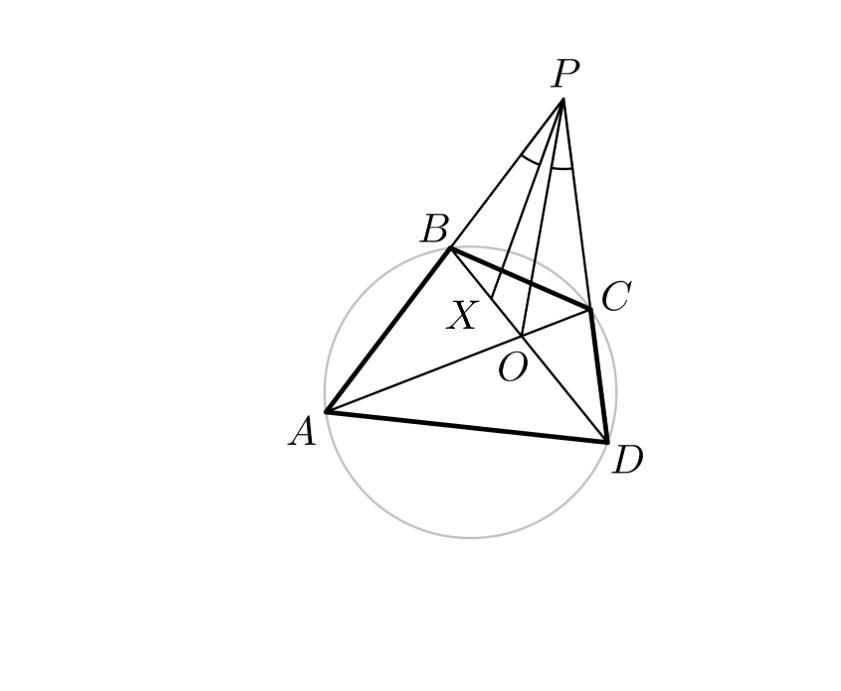
СРОЧНО! Нужна помощь. Можно без решения. Диагонали вписанного четырёхугольника ABCD пересекаются в точке O. Прямые AB и CD пересекаются в точке P. Точка X на отрезке BD такова, что ∠APX=∠DPO. Известно, что AC=10, BD=11, OC=3. Найдите длину отрезка DX.
Приложения:
antonovm:
Я уже решал эту задачу - https://znanija.com/task/45078183
Ответы
Ответ дал:
1
По формуле ШТЕЙНЕРА
BX/DX * BO/OD = (BP/PD)^2
но так как BP/PD = BC/AD = BO/AO (из-за того что ABCD вписанный BPC, APD подобны)
BX/DX * BO/OD = (BO/AO)^2
BX/DX = BO*OD/AO^2
AO=10-3=7
по теореме о секущей BO*OD=AO*OC = 7*3=21
BX=11-DX
BX/DX = 21/7^2
(11-DX)/DX=21/49
DX=77/10
Можно заметить, что APC и BPD подобны (по 2 углам), (что значит AC/PC = BD/PB); поэтому при отражении относительно биссектрисы угла APD С -> C' на AP; B-> B' на DP, O -> O' на PX; (из за равенства отмеченных углов, ну то есть изогональ); C'B' II AD, => PC'O' подобен PBX => PCO подобен PBX; CO/PC = BX/PB; => CO/AC = BX/BD; 3/10 = BX/11; BX = 3,3; DX = 11 - BX = 7,7
А что за формула Штейнера? справа стоит двойное отношение... почему не знаю?
Блин, зачем B'? вот что значит делать в уме без рисунка. A->A' ...ну идея понятна
Не, мне точно надо отдохнуть. Вся эта ерунда с отражением относительно биссектрисы - просто мусор в голове, можно конечно, но не нужно совсем. Треугольники PBX и PСO просто подобны по 2 углам точно также, как APC и BPD; ∠ABD = ∠ACD; =>∠PBX = ∠PCO; ну, и дальше две пропорции - из одной пары и из другой, - надо поделить друг на друга. См. первый комментарий.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад