Предмет: Математика
Автор: ansty1998
Вопрос задан 7 лет назад

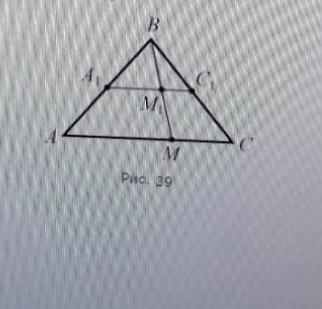
в треугольнике АВС отрезок А1С1 параллелен основанию АС, прямая ВМ пересекает отрезок А1С1 в точке М1 (рис. 39). Докажите, что А1М1 : АМ = М1С1 : МС и ВМ1 : ВМ = ВА1 : ВА

Приложения:

Аноним: Докажите подобие треугольников, и всё.

ansty1998: А как доказать это?

Аноним: <МВС- общий для ∆МВС и ∆ М1ВС1. <МСВ=<М1С1В, соответственные углы при паралельных прямых М1С||МС секущей ВС. ∆МВС~∆М1ВС1, по первому признаку (два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобные) В подобные треугольниках соответственные стороны прямо пропорциональны.

Аноним: ВМ1/ВМ=ВС1/ВС.

Аноним: Теперь доказать подобие других двух ∆А1ВМ1~∆АВМ, точно так же по первому признаку отношение А1В/АВ=ВМ1/ВМ.

ansty1998: Спасибо, но как доказать, что А1М1:АМ = М1С1:МС?

Аноним: ∆АВС~∆А1ВС1,

ansty1998: Но я все равно не помнишь

ansty1998: Но я все равно не понимаю, как это связать :(