В прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 22°. Найдите больший угол данного треугольни. ка. Ответ дайте в градусах.
спасибо большое
orjabinina аватарку сменили? :) в прямоугольном треугольнике между медианой и высотой ∠HCO = ∠B -∠A =22°; (B - больший); ну и ∠B +∠A = 90°; система для 5 класса. Тут полезно запомнить, что высота из С в любом треугольнике образует с радиусом описанной окружности (тоже из С) угол ∠HCO =∠B -∠A; это и задачка хорошая, хоть и совсем простенькая (эти отрезки изогональны, то есть симметричны относительно биссектрисы, ну или образуют одинаковые углы с боковыми сторонами)
Ответы
Ответ дал:
1
Ответ:
∠ABC = 67°
Объяснение:
Дано: ΔABC - прямоугольный
∠C=90°
СО - биссектриса
CH - высота
∠OCH = 22°
Найти: бОльший угол ΔABC
Решение:
Т.к. биссектриса делит угол пополам, а она проведена из прямого угла,следовательно ∠ACO=∠OCB=90°:2=45°
Угол ∠OCB состоит из углов ∠OCH и ∠HCB. Из этого мы делаем вывод,что ∠HCB=∠OCB-∠OCH = 45°-22°=23°
ΔСНВ - прямоугольный,т.к. CH - высота. Из этого ∠ABC=90°-∠HCB=90°-23°=67°
ΔСНВ - прямоугольный(по условию).Из этого ∠ВАC=90°-∠ABC=90°-67°=23°
Мы видим, что ∠ABC > ∠ВАC => в ответ пишем градусную меру угла ∠ABC
Приложения:
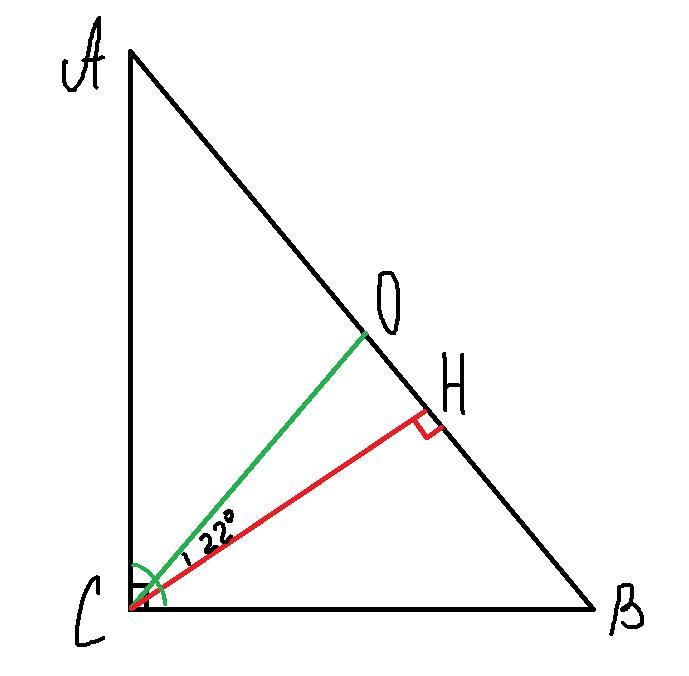
Там в условии угол с медианой, а не с биссектрисой. Конечно, разница всего в 2 раза, не принципиально :) (шучу, я видел, тут была и задача с биссектрисой, да и суть решения та же, просто ответ не на тот вопрос)
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
10 лет назад
https://znanija.com/task/24921445