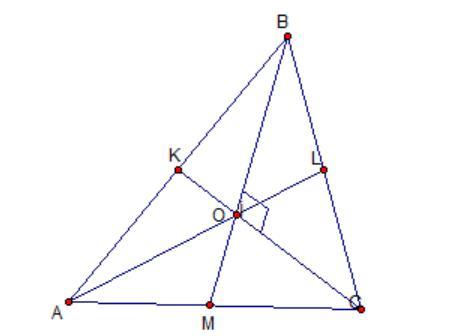
В треугольнику АВС медианы ВМ и СК перпендикулярные и пересекаются в точке О. Найдите отрезок АО, если ВМ=36 см и СК =15
stellaichme:
Если я думаю о том ответе, о котором вы говорите, то это неправильный ответ
Вам известно какой ответ должен быть?
Нет
Точнее знаю, что там должна быть цифра, а в том ответе о котором я говорю только доказательство
Какой ответ?
Треугольник АВС, АК=ВК, АМ=СМ, если прямые которые пересекают стороны угла отсекают на его сторонах равные отрезки то прямые параллельны, КМ параллелна ВС, КМ-средняя линия, угол МОК=уголВОC как вертикальные, уголКМО=уголОВС как внутренние разносторонниеТреугольник КОМ подобен треугольнику СОВ по двум углам Вот))
Вот этот
я имею ввиду числовой ответ. Какой в книге
Этого ответа нет
26 см
Ответы
Ответ дал:
3
Точка пересечения медиан треугольника делит каждую из этих медиан в отношении 2 : 1, считая от вершины треугольника.
BO = 2/3 * BM = 2/3 * 36 = 24 см
CO = 2/3 * CK = 2/3 * 15 = 10 см
ΔBOC - прямоугольный. По теореме Пифагора:
BC² = BO² + CO² = 676 откуда BC = 26 см
Пусть AL - третья медиана этого треугольника.
BL = CL = 1/2 * BC = 13 см. Поскольку L - середина ВС(гипотенузы) прямоугольного треугольника BOC, то OL = BL = CL = 13 см.
AO : OL = 2 : 1
AO = 2OL = 2 * 13 = 26 см
Ответ: 26 см.
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад