Question

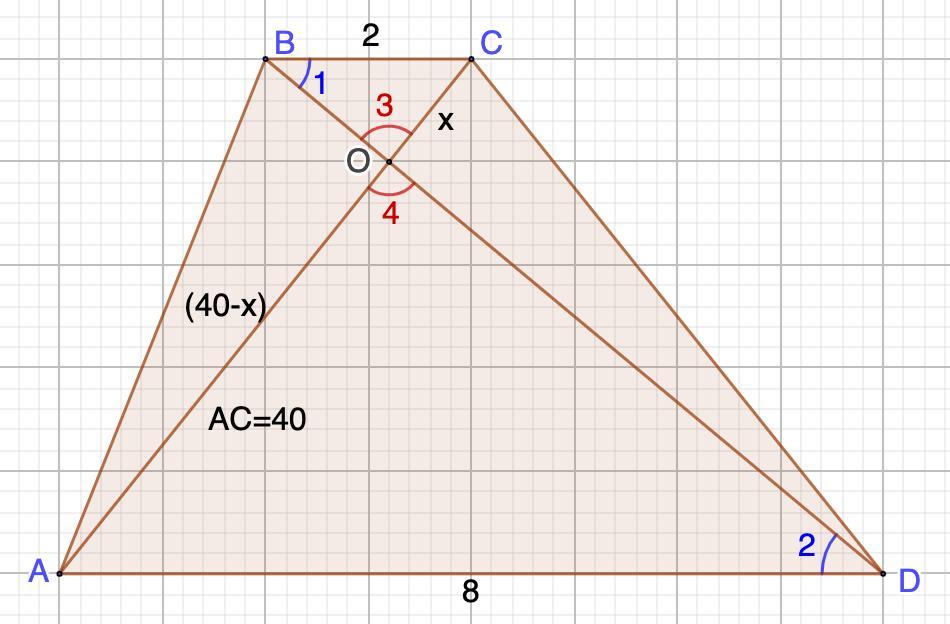
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC = 2, AD = 8, AC = 40. Найдите AO.​

Answer 1

Ответ:

АО = 32 ед.

Пошаговое объяснение:

Надо найти отрезок АО.

Дано: ABCD - трапеция;

АС и ВD - диагонали;

BC и AD - основания;

ВС = 2; AD = 8; AC = 40.

Найти: АО.

Решение:

Для того, чтобы найти АО, надо доказать подобие ΔВСО и ΔAOD.

1. Рассмотрим  ΔВСО и ΔAOD.

∠1 = ∠2 (накрест лежащие при ВС || AD и секущей BD)

∠3 = ∠4 (вертикальные)

⇒ ΔВСО ~ ΔAOD (по двум углам)

2. Запишем отношение сходственных сторон:

• Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов.

$\displaystyle \frac{BC}{AD}=\frac{OC}{AO}\;\;\;\;\;(1)$

ОС и АО нам неизвестны. Поэтому ОС примем за х. Тогда:

$\displaystyle OC=x;\;\;\;\;\;\Rightarrow \;\;\;\;\;AO=40-x$

Подставим значения BC = 2; AD = 8; OC = x; AO = 40 - x в выражение (1):

$\displaystyle \frac{2}{8}=\frac{x}{40-x}$

Используем основное свойство пропорции и решим уравнение:

• Произведение крайних равно произведению средних.

$\displaystyle 2(40-x)=8*x\\\\80-2x=8x\\\\80=10x\;\;\;|:10\\\\x=8$

Теперь можем найти АО:

$\displaystyle AO=40-x=40-8=32$

Значит искомый отрезок

АО = 32 (ед)