Двойной интеграл, реите пожалуйста
Приложения:
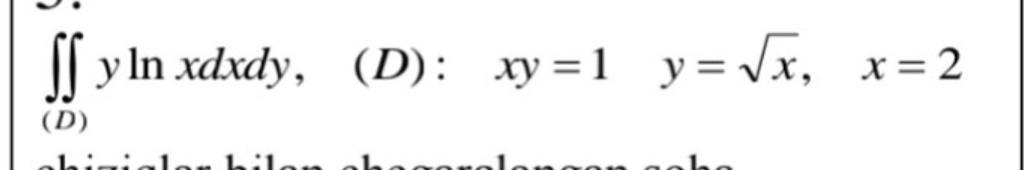
DK954:
А у вас есть на него ответ?
Если ты есть в вк, тогда зайди в сообщество "Клуб любителей брать интегралы", там тебе помогут его решить.
Ответы
Ответ дал:
0
Ответ:
Объяснение:
ну, если я правильно расставила пределы (определила область D),то тогда получим вот что
считаем внутренний интеграл
теперь считаем внешний интеграл
я не писала подробный вывод неопределенных интегралов, но, если есть желание, можно проверить - ответ именно такой
(первый и второй интегрируем по частям в первом f=ln(x), g=x²/2, во втором f=ln(x), g=-1/x)
Приложения:
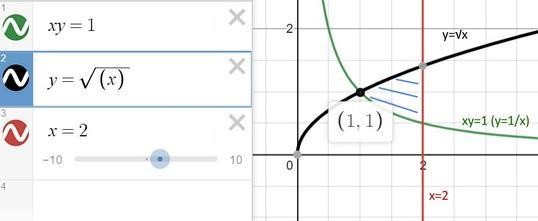
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад