Помогите пожалуйста решить!!
Приложения:
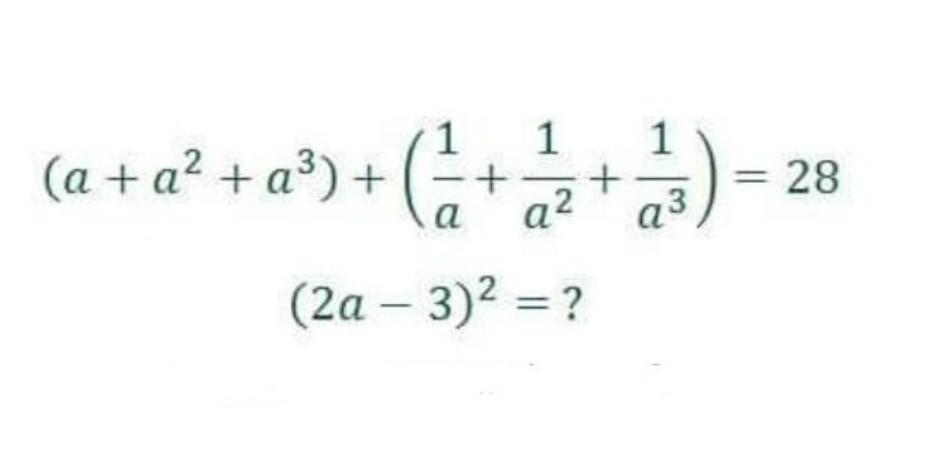
добавьте ответ
Это для последнего вопроса который удалили , но Метр Эйлера как понял не работает,всё сложновато-_-
а понятно
ф(200)×ф(500)×10000= 199/200 ×499/500×10000 как понял метод Эйлера должен быть так и это должен быть равно 167 , но здесь таким числом не пахнет скажем в английском пример было такой 3⁴⁰⁰ хочет последние 3 цифры , 1000×ф(1/2)×ф(4/5)=400 тогда 3⁴⁰⁰1mood = 001 последние 3 цифры
Либо я вообще метод не понял
Или степень должен быть чётной.
1 мин 500 не простой число , я не правильно написал года.
тогда* пойду ещё глянуть.
Этот задания кажется по такой логике в числителе получим а⁶+а⁵+а⁴+а²+а+1=28 а³ , а⁴(а²+а+1)+а²+а+1=28а³ , а²+а+1=t ..... а⁴t+t=28a³, сейчас надо думать какую перемену делать.
Ответы
Ответ дал:
5
Ответ:
5
Объяснение:
Решение на фото
Приложения:
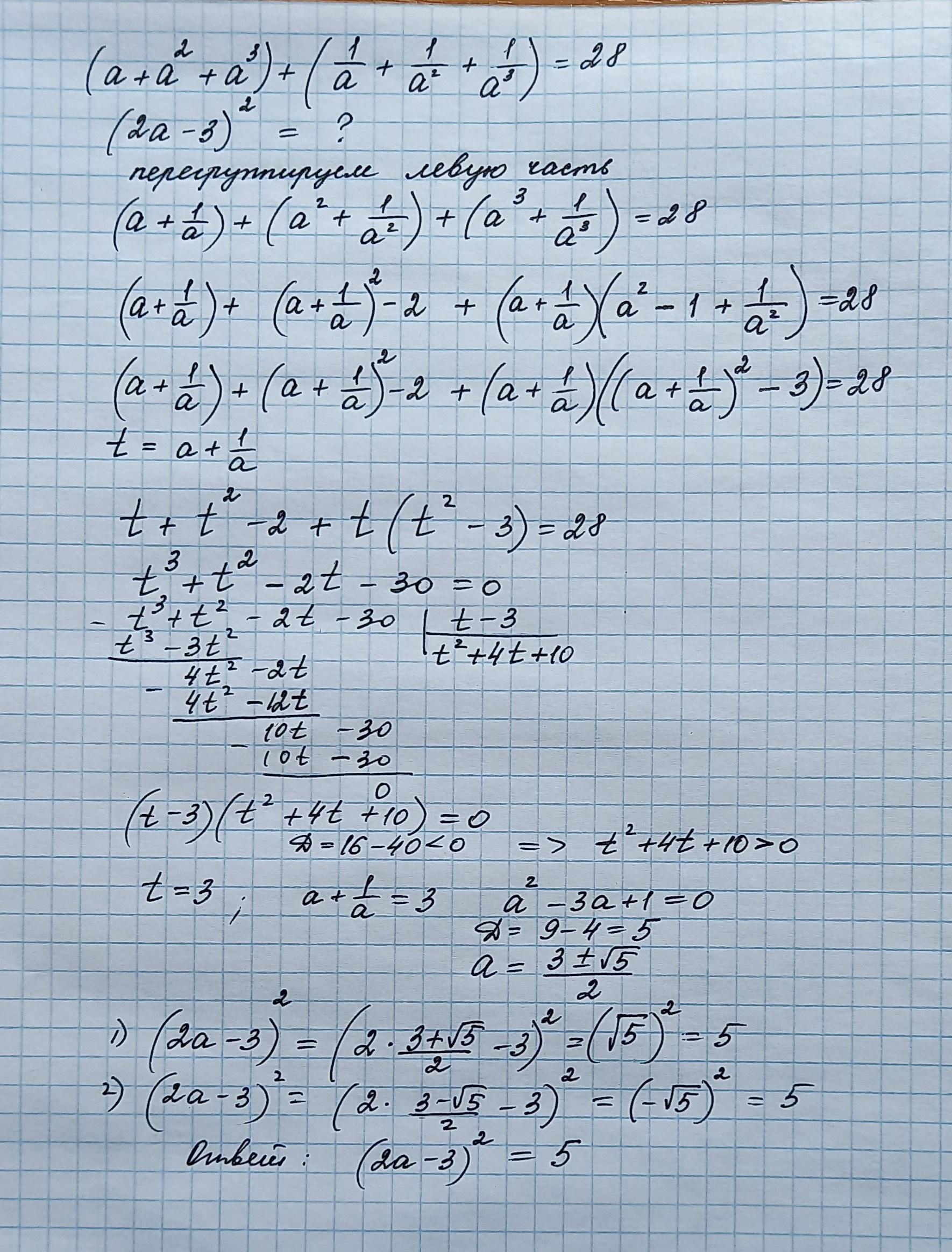
помогите пожалуйста
помогите пожалуйста с алгеброй вопрос в профиле
Вас заинтересует
3 года назад
3 года назад
8 лет назад
9 лет назад
Например:
9 = 3 2 , φ ( 9 ) = 9 * (1-1 / 3) = 6
4 = 2 2 , φ ( 4 ) = 4 * (1-1 / 2) = 2
15 = 3 * 5, φ ( 15 ) = 15 * (1-1 / 3) * (1-1 / 5) = 15 * (2/3) * (4/5) = 8
Теорема Эйлера обобщает теорему Ферма на случай, когда модуль не является простым. В нем говорится, что:
если n - натуральное число и a, n взаимно просты, то a φ (n) ≡ 1 mod n, где φ (n) - функция Эйлера. Понимаешь что это?