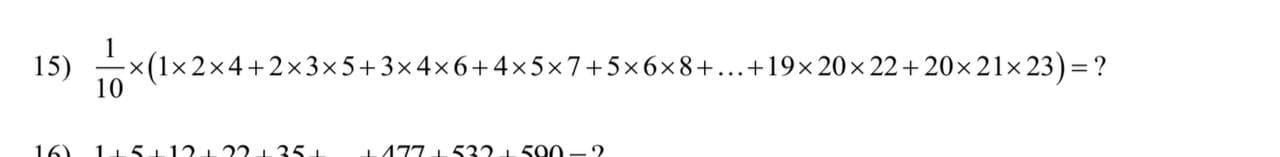Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
Сначала найдем вспомогательную сумму
Нетрудно заметить, что
Тогда
Домножив на , получим
Обозначим .
Вернемся к исходному условию и преобразуем его:
С учетом (1), получим
неужели так все сложно задача просто задача за 7 класс
Эх, придется задать стандартный вопрос спамера: а из какой темы задание? )
Вообще, если это 7 класс, мое решение будет действительно избыточно, я, по сути, доказал более общий случай, и должно существовать более простое решение
Вообще, если это 7 класс, мое решение будет действительно избыточно, я, по сути, доказал более общий случай, и должно существовать более простое решение
И такой вопрос: Вам известны формулы 1^k+2^k+...+n^k? Если да - то их использование и буде простым решением
да известны задача эта олимпиадная но олимпиада уже закончилась
Тогда все просто. Каждое из слагаемых в скобках равно n(n+1)(n+3)=n^3 + 4 n^2 + 3 n. Собственно, остается найти S_3+4S_2+3S_1, где S_i - сумма 1^i+...+20^i, и умножить на 1/10
спасибо
Но если выводить эти формулы - решение будет значительно длиннее моего, поэтому я выбрал указанный в ответе способ
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад