Помогите пожалуйста
Решите уравнение:
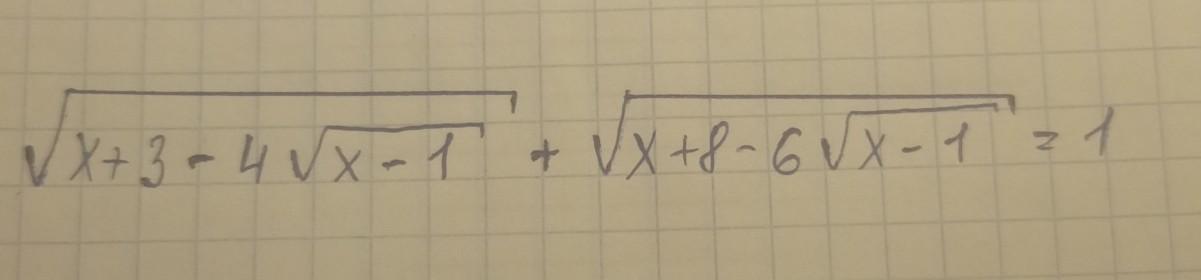
Ответы
Ответ:
[ 5 ; 10 ]
Объяснение:

с рисунком и объяснениями
Ответ:
x ∈ [5;10] в другом виде это выглядит как
Объяснение:
Сначала решим первый корень:
Если приглядеться, то можно заметить удвоенное произведение 2 и под корнем:
Это смахивает на квадрат под корнем. Но квадрат будет x-1, а не x
и квадрат 2 будет 4, а не 3. Но постойте, x+3 это же (x-1)+4. Подставляем:
И ещё немного изменяем:
Всё, теперь тут прекрасно виден квадрат разности:
Теперь заменяем корень из квадрата разности на модуль разности
Теперь решаем второй корень. Тут точно так как и в первом корне:
Для начала заменим на t:
При этом мы точно знаем, что , ведь t=
, а корень всегда либо положителен, либо равен нулю.
Для решения этого уравнения переберём 4 варианта:
1) и
2) и
3) и
4) и
Не забывая, что не зависимо от вариантов.
1) Оба подмодульных выражения положительны, значит модули можно открыть со знаком + :
Правило соблюдено, но заменим t на
позже.
2) Первое подмодульное выражение положительно, открываем со знаком + как и в первом варианте, но второе подмодульное выражение отрицательно, открываем его со знаком - :
Когда в ответе такой ответ- значит t равно любому числу. Но мы помним, что и то, что в данном варианте
и
В итоге получаем, что
3) Тут всё наоборот. Первое подмодульное выражение меньше нуля, а второе больше:
Это неверно, -1 не равна 1, а значит и у этого варианта корней нет.
4) Оба модульных выражения не положительны, а значит открываются эти модули со знаком - :
Правило соблюдено.
Объединяя все ответы мы получаем ответ:
Пришло время заменить t на .
возведём всё в квадрат:
Прибавляем 1 и получаем окончательный ответ:
Ответ: x ∈ [5;10]
На биссектрисе AL треугольника ABC как на диаметре построена окружность, проходящая через вершину C треугольника и пересекающая сторону AB в точке K. Найдите CK,если AC=28,BL=125.