Question

Ниже скриншот..........

Answer 1

Ответ:

AK=11

Объяснение:

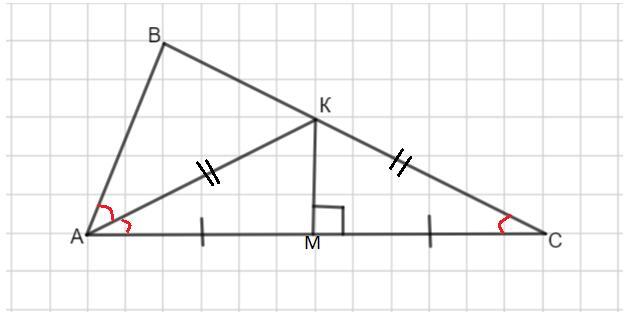
В треугольнике АВС проведена биссектриса  АК. Тогда

∠ВАК=∠КАС.

Если МК - серединный перпендикуляр к стороне АС, то КМ⊥АС и АМ=МС.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов отрезка. Значит, АК=КС и Δ АКС - равнобедренный.

У равнобедренного треугольника углы при основании равны. Тогда

∠КАС=∠КСА.

ΔАВС подобен ΔКВА по двум углам: ∠В- общий, ∠ВАК=∠ВСА.

Составим пропорцию:

$\dfrac{AB}{BK} =\dfrac{BC}{AB}$

По основному свойству пропорции: произведение крайних членов равно произведению средних членов верной пропорции.

$AB\cdot AB=BK\cdot BC\\AB^{2} =BK\cdot BC.$

И равенство доказано.

б) Пусть ∠КАС=∠КСА=∠ВАК=α.

По теореме синусов: стороны треугольника пропорциональны синусам противолежащих углов.

$\dfrac{AB}{sinC} =\dfrac{BC}{sinA} ;\\\\BC=\dfrac{30 \cdot sin2\alpha }{sin\alpha } =\dfrac{30\cdot2\cdot sin\alpha\cdot cos\alpha }{sin\alpha } =60cos\alpha$

По условию

$sin\alpha =\dfrac{4}{5} .$

Найдем косинус угла, применяя основное тригонометрическое тождество

$sin^{2} \alpha +cos^{2} \alpha =1;\\cos^{2} \alpha= 1-sin^{2} \alpha ;\\cos\alpha =\pm\sqrt{ 1-sin^{2} \alpha}$

Так как угол α - острый, то косинус принимает положительное значение.

$cos\alpha =\sqrt{1-\left(\dfrac{4}{5}\right)^{2} } =\sqrt{1-\dfrac{16}{25} } =\sqrt{\dfrac{25-16}{25} } =\sqrt{\dfrac{9}{25} } =\dfrac{3}{5}$

Тогда

$BC=60\cdot \dfrac{3}{5} =\dfrac{5\cdot12\cdot3}{5} =36$

По доказанному

$AB^{2} =BK\cdot BC.\\\\BK= \dfrac{AB^{2} }{BC} ;\\BK= \dfrac{30^{2} }{36} =\dfrac{30\cdot30}{36} =\dfrac{5\cdot6\cdot5\cdot6}{6\cdot6} =5\cdot5=25$

$KC= BC-BK;\\KC= 36-25=11;\\AK=KC=11$