в прямоугольнике длины сторон которого равны 8 и 2 проведены биссектрисы всех углов до взаимного пересечения. Найдите площадь четырехугольника который образован этими биссектрисами. Ответ :18 . МОЖНО РИСУНОК С ОБЬЯСНЕНИЕМ, ПРОШУУУУ. ПОМОГИТЕ ПОЖАЛУЙСТА.

Ответы

Ответ дал: Аноним

Ответ:

18ед²

Объяснение:

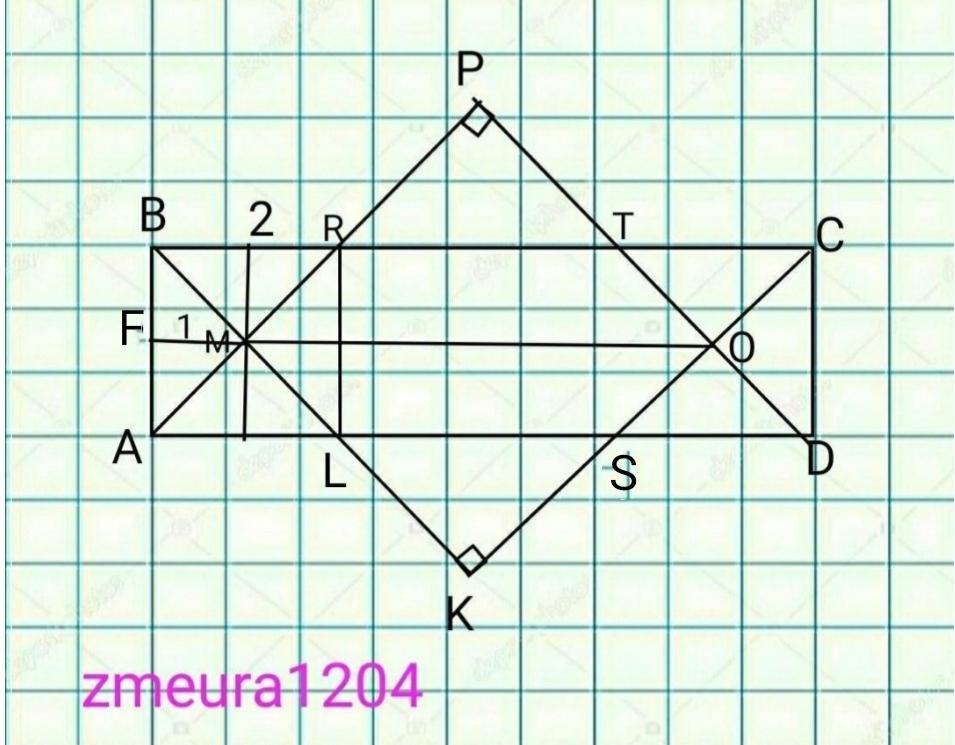
AB=BR=2 ед биссектрисса отсекает, отрезок ВR равный стороне АВ

АВRL- квадрат (все углы по 90°, две смежные стороны равны 2.)

FM=1/2*BR=2/2=1 ед

MO=AD-1-1=8-2=6

MPOK- квадрат

S(MPOK)=МO²/2=6²/2=36/2=18 ед²

Приложения:

Аноним: кааааак ты это сделааал????

Аноним: Биссектрисса АР отсекает от стороны ВС сторону АВ; Биссектрисса РD отсекает от стороны ВС сторону СD.

Аноним: В прямоугольнике углы 90°; биссектрисса делит угол пополам значит ∆АВR- равнобедренный прямоугольный треугольник. ТСD- равнобедренный прямоугольный треугольник.

Аноним: МРОК- квадрат. Если соединить АВR и точку внизу, то это тоже квадрат. AR-диагональ квадрата. Формула нахождения диагонали квадрата AR=AB*√2=2√2.

Аноним: Завтра исправлю решение, если все же будет не понятно.

Аноним: спасибо

Вас заинтересует

Английский язык

2 года назад

помогите пожалуйста,дам 20 баллов

Английский язык

2 года назад

"Tasteless" можно употреблять в сочетании "безвкусная одежда"?

Русский язык

3 года назад

Прошу просто выполнить задания к тексту. Их мало. Хотя-бы посмотрите какие! Заранее СПАСИБООО))) 1)Начинающий натуралист шел вдоль поросшей молодым леском лощины.2) Здесь было еще по-утреннему свежо