Предмет: Геометрия
Автор: Аноним
Вопрос задан 7 лет назад

В параллелограмме ABCD угол BAD равен 60 градусов, а биссектриса этого угла делит сторону BС на отрезки равные 4 и 6. Найдите площадь параллелограмма.

guvanch021272: Пусть биссектриса это отрезок AE. Если BE=4, EC=6 тогда ответ ответ будет отличаться от случая BE=6, EC=4. Порядок не указан. Еxample is not correct

Ответы

Ответ дал: Аноним

Решение задания прилагаю

Приложения:

Аноним: спасибооо .

Аноним: Если рассматривать второй случай, когда ВК=6, КС=4, тогда AB=6 и S=6*10*|/3 /2=30|/3. Посмотрите в условии сторону делит на отрезки считая от тупого угла? Обычно так пишут. Если этого нет, то рассматриваем 2 случая.

Ответ дал: Пеппер

Ответ:

20√3 ед²

Объяснение:

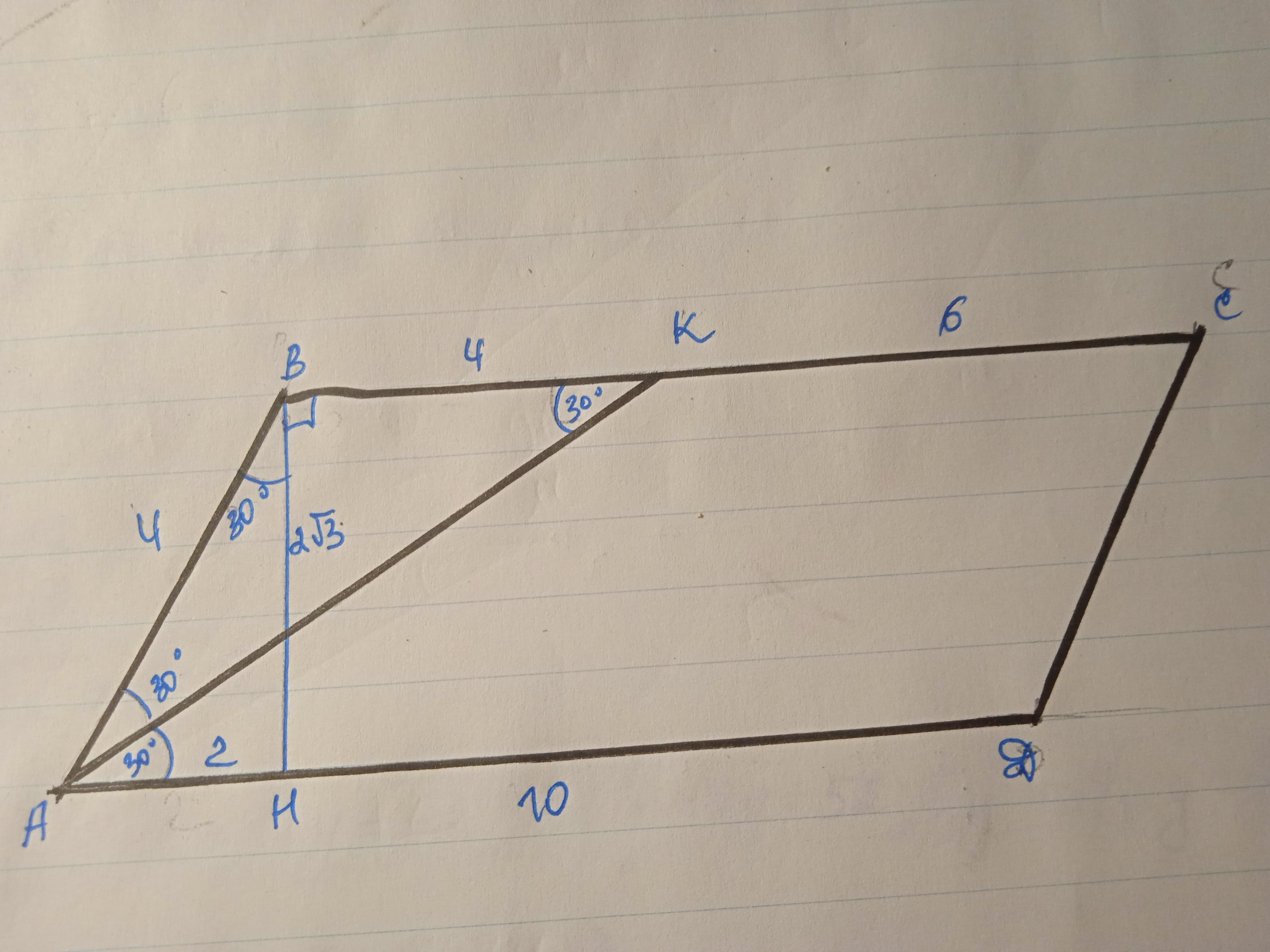
Дано: АВСD - параллелограмм, ∠А=60°, АК - биссектриса, ВК=4, СК=6. Найти S(ABCD).

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

ΔАВК - равнобедренный, АВ=ВК=4.

Проведем высоту ВН, ΔАВН - прямоугольный.

∠ВАН=60°, тогда ∠АВН=30°, т.к. сумма острых углов прямоугольного треугольника составляет 90°

АН=1/2 АВ по свойству катета, лежащего против угла 30°

АН=2.

Найдем ВН по теореме Пифагора